1. finance
2. investing
3. stocks

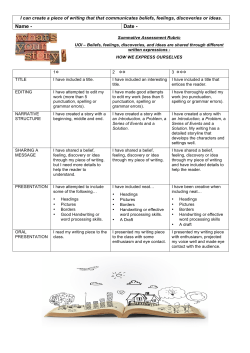
Belief Risk and the Cross-Section of Stock
Returns∗
Rajna Gibson Brandon† and Songtao Wang‡
March 26, 2015
Abstract
We examine whether belief risk arising from stochastic fluctuations in the average
belief of investors is priced. We construct a market-wide belief measure with analysts’
EPS forecast data and an EPS forecasting model. Market-wide belief primarily captures the average subjective opinion of institutional investors and represents a source
of commonality in stock returns. The average return on stocks with high exposure to
belief risk is 6.35%/year higher than that of stocks with low exposure. This positive
∗
We thank Yakov Amihud, Tim Baldenius, Michael Brennan, Stephen Brown, Francois Degeorge, Jerome
Detemple, and Jeffrey Wurgler for helpful comments and discussions, as well as participants of the 2013
NFA Annual Conference and the finance seminar at Shanghai Jiao Tong University. The financial support of
the Swiss National Science Foundation and the NCCR-Finrisk Project C1 “Credit Risk and Non-Standard
Sources of Risk in Finance” is greatly acknowledged. All errors are ours.
†
Rajna Gibson Brandon is the Swiss Finance Institute (SFI) Chaired Professor of Finance at the Geneva
Finance Research Institute, University of Geneva, Geneva, Switzerland. Email: rajna.gibson@unige.ch
‡
Songtao Wang is Assistant Professor at the Antai College of Economics and Management, Shanghai Jiao
Tong University, Shanghai, China. Email: wangsongtao@sjtu.edu.cn
1
relation between belief risk and expected stock returns holds after accounting for traditional risk factors and is prominent among large-cap stocks.
Keywords: Analysts’ EPS Forecasts; Asset pricing; Belief Risk; Commonality.
JEL codes: G11; G12.
2
I
Introduction
Heterogeneity in investor beliefs plays an important role in explaining the formation of stock
prices and it is well known that asset pricing models incorporating such heterogeneity are
able to better account for stylized facts characterizing stock returns and to rationalize the
existence of trading volume and of stock market bubbles and crashes. So far, the dominant
stream of the literature on heterogeneous beliefs has been studying the impact of the dispersion in investor beliefs and its ability to overcome the empirically documented limitations of
representative agent pricing models1 . While individuals, whether they are investors, portfolio managers, financial analysts or economists, are known to disagree, it is also interesting
to observe that financial markets thrive at conforming and relying on consensus forecasts,
for instance, to extract information regarding market pessimism or optimism for trading
and portfolio allocation purposes. This explains the popularity of various retail investors’
sentiment measures developed both in academic (described in the literature review section
below) and in business settings to guide investors buying and selling decisions. Hence, the
first moment of the distribution of investors’ heterogenous beliefs seems to matter as well.
Motivated by this last observation, another less explored stream of the literature on heterogeneous beliefs theoretically examines the impact of the average belief of investors on
the formation of asset prices. In particular, Jouini and Napp (2007) develop a model in
which investors possess heterogeneous beliefs about the growth rate of aggregate wealth.
They show that, in the heterogeneous beliefs setting, the equilibrium asset price positively
1
The role of the dispersion in investor beliefs has been studied in particular by Harrison and Kreps
(1978), Varian (1985), Harris and Raviv (1993), Detemple and Murthy (1994), Zapatero (1998), Basak
(2000), Scheinkman and Xiong (2003), Buraschi and Jiltsov (2006), Li (2007), Pavlova and Rigobon (2007),
Dumas, Kurshev, and Uppal (2009), Xiong and Yan (2010).
3
depends on the average belief defined as the risk tolerance weighted average of the individual
beliefs when investors are cautious: an optimistic average belief increases the equilibrium
risky asset price. Likewise, Kurz and Motolese (2011) derive a very similar result, namely
that the price of a risky asset is a linear function of the equally-weighted average of investors’
beliefs about the asset’s payoffs, with a positive beta coefficient for the average belief factor.
When average or consensus beliefs about the prospects of financial markets are shown
to matter and positively affect stock prices, it seems worthwhile to explore what happens
when unexpected shocks alter those average beliefs and, in particular, whether they depress
stock prices in a similar way as unexpected liquidity shocks do. Yet, little is currently known
regarding the impact of unexpected average belief shocks on stock returns. Let us define the
market-wide belief measure, and call it the “market-wide belief”, as the cross-sectional mean
of the average beliefs of investors about the future earnings of all risky stocks. One could
view this belief measure as representing the average level of optimism or pessimism currently
held by market participants regarding the short term earnings prospects of a representative
stock. If the market-wide belief measure represents an omitted source of commonality, will its
innovations depress stock prices? This main question lies at the core of our study. To answer
this question, we first show that investors’ beliefs and thus the market-wide belief evolve
stochastically over time. In Kurz and Motolese’s (2011) model, individual investors’ beliefs
about future asset payoffs are assumed to follow a stochastic AR(1) process. Along the same
vein, De Long et al. (1990) assume that noise traders’ expectations regarding asset returns
are subject to the impact of not fully predictable and stochastic sentiment. Empirically,
this conjecture is also supported by the fact that other sentiment indices developed by,
for example, Baker and Wurgler (2006, 2007) and Barone-Adesi et al. (2013) fluctuate
stochastically over time. Second, we document that the market-wide belief represents a
4
source of commonality affecting individual stocks’ average beliefs.
The finding that the market-wide belief is a random source of commonality motivates
us next to posit and test our main hypothesis, namely whether market-wide belief risk,
thereafter referred to as “belief risk” arising from stochastic fluctuations in the market-wide
belief, is priced in stock returns:
The Belief Risk Hypothesis: Stocks with Higher Exposure
to Belief Risk Earn a Higher Expected Return.
This empirical study focuses on the U.S. stock market and relies on the actual EPS and
analyst EPS forecast data provided by I/B/E/S (Institutional Brokers’ Estimate System) to
construct a market-wide belief measure. First, we adopt the econometric model proposed
by Brown and Rozeff (1979) to objectively forecast each stock’s EPS, and then compute the
average belief of investors for a stock as the mean analyst EPS forecast minus the one derived
from the Brown and Rozeff (1979) model. The market-wide belief is defined as the crosssectional mean of the price-scaled average beliefs across all sample stocks. Innovations in the
market-wide belief are then estimated as the residuals of an AR(6) model that simultaneously
eliminates the macro-economic components from the market-wide belief’s evolution. To test
our main hypothesis, we finally form portfolios based on the sensitivity of each stock’s excess
returns to innovations in the market-wide belief.
Our main findings can be summarized as follows: the average return delivered by stocks
with high exposure to belief risk is significantly higher than that of stocks with low exposure,
this positive relation being particularly strong in magnitude for large-cap and low to middle
book-to-market stocks. An investment strategy that is long in stocks with high exposure to
belief risk and short in stocks with low exposure to belief risk yields a significant alpha of
5
6.23%/year with the Fama and French (1993) model and 6.10%/year with the Carhart (1997)
model, meaning that the traditional three- and four-factor models cannot fully explain this
pattern in stock average returns. We also show that accounting for liquidity risk by using
the Pastor and Stambaugh (2003) liquidity risk factor does not meaningfully affect these
abnormal returns. These results are robust to: i) an alternative EPS forecasting model; ii)
value-weighted stock portfolios; iii) accounting for divergence of analysts’ forecasts; iv) a subsample analysis. Finally, we examine the determinants of a stock’s exposure to belief risk and
find that it increases with the stock’s market beta, volatility, turnover rate, and sale-to-asset
ratio and decreases with size, book-to-market, momentum, and analyst coverage.
This paper provides several contributions to the growing literature on the impact of
investors’ heterogeneous beliefs on stock returns:
First, the results show that stochastic fluctuations in the market-wide belief is a priced
source of risk distinct from other sources of systematic risk accounted for by standard asset
pricing models. The issue of whether the risk arising from these stochastic fluctuations in
the market-wide belief is cross-sectionally priced in stock returns, although economically
important, has so far been neglected in the empirical asset pricing literature and this study
attempts to bridge that gap.
Second, this paper provides yet another potential explanation for the equity premium
puzzle documented first by Mehra and Prescott (1985): part of the excess equity premium
may represent a compensation for investors who have to bear systematic belief risk.
Finally, we show that the market-wide belief measure that we construct primarily captures
the average subjective opinions of an important category of investors, namely institutional
investors. So far, most sentiment measures, as for instance, the closed-end fund discount (Lee
6
et al., 1991) or the Baker and Wurgler (2006) sentiment index, were designed to reflect small
investors’ sentiment. O’Brien and Bhushan (1990) conjecture that sell-side research analysts
act as information intermediaries for institutional investors. Moreover, studies such as Brown
et al. (2012), Chen and Cheng (2006), Costelle and Hall (2011), Fang and Kosowki (2007),
Franck and Kerl (2013), and Malmendier and Shanthikumar (2009) show that institutional
investors rely on the information provided by research analysts to make their investment
decisions. Particularly, both Franck and Kerl (2013) and Malmendier and Shanthikumar
(2009) document a positive correlation between changes in institutional investors’ equity
holdings and changes in analysts’ EPS forecasts. Based on these studies, it is reasonable to
conjecture that the market-wide belief measure that we construct using the actual EPS and
analyst EPS forecast data captures the average subjective opinions of institutional investors
rather than retail investors. Thus, it is not surprising to observe that the market-wide belief
measure is only weakly correlated with other popular sentiment indices.
II
Literature review
While an abundant literature has examined the effect of the dispersion in investors’ subjective
beliefs on stock prices, the focus on the impact of the average investors’ beliefs remains quite
limited.
Jouini and Napp (2007) show that the introduction of heterogeneous beliefs in an otherwise standard competitive complete market economy has two distinct effects: the first effect
is associated with a change of the objective expectation to the aggregate belief defined as a
weighted average of the individual subjective beliefs, and the second effect is represented by
a discount factor proportional to the belief dispersion. In their heterogeneous beliefs setting,
7
the equilibrium asset price is increasing in the aggregate belief about the growth rate of
aggregate wealth when investors are cautious while the discount factor lowers the risky asset
price.
Kurz and Motolese (2011) develop a model in which investors differ in their beliefs about
future asset payoffs. By assuming that individual investors’ beliefs follow a stochastic AR(1)
process, they show that the equilibrium asset price is positively related to the average belief
of investors about future prospects of asset payoffs.
On the empirical side, Diether et al. (2002) show a negative cross-sectional relation between the dispersion in investor beliefs approximated by the disagreement among analysts’
earnings forecasts and expected stock returns, supporting Miller’s (1977) view that the dispersion in investor beliefs is priced at a premium in the presence of short-sale constraints.
Using the diversity in analysts’ forecasts measure of BKLS (1998), however, Doukas et al.
(2006) obtain an opposite result, and their finding is consistent with the predictions of models of Williams (1977), Mayshar (1983), and Epstein and Wang (1994) who posit that the
dispersion in investor beliefs is a priced source of risk. Anderson et al. (2005) provide further
evidence that heterogeneity in investor beliefs is a priced risk factor and show that incorporating investors’ beliefs can improve the performance of traditional asset pricing models.
What makes our paper different from these empirical studies is that we examine the impact of the average belief of investors (i.e. the first moment of the distribution of investors’
heterogeneous beliefs) while those authors instead explore the impact of the dispersion in
investor beliefs (i.e. the second moment of the belief distribution).
Baker and Wurgler (2006) study how the aggregate sentiment of investors affects the
cross-section of stock returns and find that the cross-section of future stock returns is condi-
8
tional on beginning-of-period investor sentiment. When sentiment is estimated to be high,
stocks that are attractive to optimists and speculators and at the same time unattractive to
arbitrageurs - small stocks, younger stocks, growth stocks, unprofitable stocks, non-dividend
paying stocks, high volatility stocks, and distressed stocks - tend to earn relatively low
subsequent returns. Conditional on low sentiment, however, these cross-sectional patterns
disappear. The difference between Baker and Wurgler (2006) and our study is twofold: first,
as will be seen in Section VI.A, the sentiment index developed by Baker and Wurgler (2006)
captures the aggregate opinion of retail investors while our market-wide belief measure primarily reflects institutional investors’ opinions; secondly, and more importantly, Baker and
Wurgler (2006) examine the cross-sectional predictability of stock returns conditional on
investor sentiment, while our aim is to study whether the risk associated with stochastic
fluctuations in the average belief of institutional investors is priced.
Ben-Rephael et al. (2012) also examine the relation between investor sentiment and
stock returns, but at the market level. Using the aggregate net flows from bond funds to
equity funds in the USA as a proxy for investor sentiment, they document a significantly
positive contemporaneous relation between monthly aggregate net flows to equity funds and
stock market excess returns and that about 85% of these price changes are reversed within
four months while the rest is reversed within ten months. Edelen and Warner (2001) and
Goetzmann and Massa (2003) obtain similar findings using higher frequency (daily) data.
Our study also relates to Lee et al. (1991) who show that stocks and closed-end funds
with high sensitivity to investor sentiment earn an extra return as a compensation for this
additional source of risk. In contrast to Lee et al. (1991), we examine a different measure
of investors’ beliefs that primarily captures the average opinion of institutional investors.
9
Furthermore, the aim of Lee et al. (1991) is to solve the closed-end fund puzzle, an issue left
unexplored in our paper.
III
Data
In light of the difficulties raised by collecting data on investors’ direct opinions, we will use
analysts’ forecasts as a proxy for institutional investors’ opinions.
The analyst forecast data are taken from the Institutional Brokers’ Estimate System
(I/B/E/S) Summary History database that contains the summary statistics for analysts’
forecasts and the date when the forecast was last confirmed to be accurate. These data are
usually disclosed on the third Tuesday of each month.2
I/B/E/S collects two categories of analyst forecast data: one concerns EPS (Earnings
Per Share) and another concerns DPS (Dividends Per Share). DPS is sensitive to a firm’s
dividend payout policy whose impact is not easy to control for in empirical studies. More
importantly, the analyst DPS forecast data only have a short history and the analyst coverage
for DPS forecasts is also low. For these reasons, we use the analyst EPS forecast data in the
following empirical analysis.3
To construct the market-wide belief measure, we also need the actual EPS data. The
actual EPS data provided by I/B/E/S are called the ‘Street’ EPS since they are tracked
by financial analysts and followed by investors. COMPUSTAT provides the data of another
category of actual EPS known as the GAAP EPS reported in firms’ financial statements.
2
Diether et al. (2002) provide a detailed description of the I/B/E/S database
3
If the payout ratios of firms are stable over time, the empirical results obtained with either the EPS or
the DPS forecasts should be similar.
10
Bradshaw and Sloan (2002) find that there exists a large and growing gap between the
‘Street’ EPS data and the GAAP EPS data since the former excludes cost items such as
‘non-recurring’ and ‘no-cash’ charges.4
The ‘Street’ EPS data are quantitatively consistent with analysts’ EPS forecasts and
hence used to construct the market-wide belief measure although the GAAP EPS data have
a longer history. The actual EPS and analyst EPS forecast data reported by I/B/E/S have
different periodicities: quarterly, semi-annually, annually, etc. This study uses the quarterly
EPS data for the following reasons: first, the analyst coverage for quarterly EPS forecasts
is higher (thus reflecting the opinions of a broader community of analysts and investors);
second, in the accounting literature, the econometric models developed to forecast earnings
are mainly intended for quarterly EPS.
Stocks used to construct the market-wide belief measure are those with fiscal quarters
ending in the months of March, June, September, and December since the majority of stocks
in financial markets belong to this category. To be included in the construction of the
market-wide belief measure, stocks should also meet other two criteria: i) have no less than
30 consecutive observations of quarterly EPS during the period March 1983 through June
2009; ii) have the analyst EPS forecast and the model-implied EPS forecast for at least one
quarter during the period August 1990 through August 2009.
Stock data such as prices, returns, trading volumes, the number of outstanding shares,
etc. are collected from the Center for Research in Securities Prices (CRSP) Monthly Stocks
Combined File that includes stocks traded on NYSE, AMEX, and Nasdaq. Only ordinary
common shares (with CRSP share code 10 or 11) are used in this study. In addition, to
4
The difference between the ‘Street’ and GAAP earnings has been discussed in Ciccone (2002), Cote and
Qi (2005), and Zhang and Zheng (2011)
11
be included in the portfolio performance analysis below, stocks should have more than 24
quarters of return observations during the period August 1991 through August 2009.5 The
accounting data and, in particular, the book values of stocks’equity, the asset values, the debt
values, the dividends, and the sales are from the COMPUSTAT-CRSP merged database.
IV
Empirical methodology
In this section, we first explain how to construct the market-wide belief measure using the
actual EPS and analyst EPS forecast data. We then show that it is a source of commonality
and abstract from its predictable and macro-economic components to construct the belief
risk factor. We also discuss the accuracy of the market-wide belief measure. Finally, we
show how to construct portfolios to test the belief risk hypothesis.
A
Econometric EPS forecasting models
In the accounting literature, earnings forecasting is an important research topic, and many
models have been developed to undertake this task. In this study, the benchmark model
used to forecast quarterly EPS is the linear time-series model proposed by Brown and Rozeff
(henceforth BR) in 1979, which takes the following form:
E(Qs ) = δ + Qs−4 + φ(Qs−1 − Qs−5 ) + θs−4
(1)
where Qs−k is the EPS for quarter s − k and s−4 is the EPS shock experienced over quarter
s − 4. Typically, the trend term δ and the coefficient φ are both positive, and the coefficient
5
The sample period for the EPS data is longer because more historical data are needed for forecasting
quarterly EPS.
12
θ is negative. An advantage of the BR model is that it contains an autoregressive component Qs−1 − Qs−5 reflecting the positive autocorrelations in seasonal differences of quarterly
earnings at the first three lags and a moving average component s−4 reflecting the negative
autocorrelation at the fourth lag.6 Moreover, the BR model also captures the seasonality
characteristics in quarterly earnings data. The main reason behind the choice of the BR
model is that, as Bathke and Lorek (1984) and Callen et al. (1996) show, it yields better
earnings forecasts than other linear time-series models and neural network models despite
the fact that quarterly earnings data are financial, seasonal, and non-linear.
For robustness purposes, we will also use the Seasonal Random Walk with Drift (henceforth SRWD) model to forecast quarterly EPS:
E(Qs ) = δ + Qs−4
(2)
Despite its simplicity, the SRWD model has been often used in previous studies such as Sadka
(2006) and Konchitchki et al. (2013) who use it to estimate unexpected earnings shocks.
In both cases, for each stock, the forecast of the one-quarter ahead EPS is derived using
the coefficients estimated with 30 quarters of actual EPS observations.
B
Market belief measure
Let Ei,j
t (EPSs ) denote investor j’s forecast of the EPS of stock i for quarter s conditional on
the information available up to time t and Ei,m
t (EPSs ) denote the forecast derived from an
econometric model, where t can be any time after the EPS for quarter s − 1 is known and
before the EPS for quarter s is publicly disclosed. Investor j’s belief gti,j about the EPS of
6
Griffin (1977) and Foster (1977) document the existence of these autocorrelations in seasonal differences
of quarterly earnings at the first four lags.
13
i,m
stock i for quarter s is defined as the difference between Ei,j
(EPSs ):7
t (EPSs ) and Et
gti,j = Eti,j (EP Ss ) − Eti,m (EP Ss )
(3)
A positive gti,j implies that investor j is optimistic relative to an econometrician about the
EPS of stock i for quarter s. The average of individual beliefs among investors, denoted by
Zit , is equal to:
Zti
M
1 X i,j
g
=
M j=1 t
M
1 X i,j
=
Et (EP Ss ) − Eti,m (EP Ss )
M j=1
i
= E t (EP Ss ) − Eti,m (EP Ss )
(4)
i
where M is the number of investors for stock i and E t (EPSs ) is the average forecast of
investors.8 Even if provided with the same set of information, investors may still form
distinct beliefs about future EPS since they treat the information in different ways, and Zit
reflects the average belief of the M investors: the higher Zit , the more optimistic the investors.
i
We use the average of analysts’ EPS forecasts provided by I/B/E/S as a proxy for E t (EPSs ),
and Ei,m
t (EPSs ) is estimated with the time-series models proposed in Section IV. A.
For stocks with fiscal quarters ending in March, June, September, and December, the
actual EPS are released respectively in the second half of April, July, October, and January.
Analysts’ EPS forecasts are usually disclosed in the middle of each month. For a stock,
as time moves towards next quarter’s EPS release date, analysts’ forecasts will gradually
contain more public information about next quarter’s actual EPS of the stock so that Zit
7
Jouini and Napp (2007) and Kurz and Motolese (2011) define an investor’s belief in a similar way.
8
In Jouini and Napp (2007) and Xiong and Yan (2010), Zit is the risk tolerance or wealth-weighted average
belief. However, data on the weights of individual risk tolerances and wealth are empirically difficult to collect
and compute. Thus, we rely on the equally-weighted average belief.
14
constructed with those forecast data is more likely to reflect objective information rather
than analysts’ subjective judgment. For this reason, we only use in this study the analyst
EPS forecast data disclosed in February, May, August, and November, that is, when analysts
possess the least information about next quarter’s EPS. This procedure shall enable us to
focus on studying the impact of the most subjective opinions regarding stocks’ quarterly
EPS.
To enable comparison across stocks, we scale each Zit by the stock price observed at the
end of previous month Pit−1 . We define the market-wide belief, denoted by Zm
t , as the
cross-sectional average of the price-scaled Zit for all stocks in the sample:
Ztm
N
1 X Zti
=
i
N i=1 Pt−1
(5)
where N is the number of sample stocks.9 By definition, Zm
t can be interpreted as a measure
of the average belief of investors about the earnings of a stock representative of the overall
m
economy, a positive Zm
t indicating that investors are optimistic. It is worth noting that Zt
only captures investors’ average subjective belief about short-term earnings.
INSERT FIGURE 1
The top graphs in Fig. 1 plot the time series of Zm
t constructed with the BR and
SRWD models during the period August 1990 through August 2009. The market-wide belief
fluctuates over time and declines sharply during economic recession periods such as the
9
The number of stocks used to construct Zm
t varies from 602 to 1629, with an increasing trend over time
during the sample period due to the fact that more stocks have been covered by analysts. In order to avoid
the effect of outliers, we exclude the top and bottom 5% of values of Zit in the construction of Zm
t . Another
robust measure of market belief is the median of Zit , and empirical results obtained with that measure are
quantitatively similar and available upon request.
15
dot.com bubble burst at the beginning of this century and the 2007-09 subprime mortgage
crisis. Panel A of Table 1 reports summary statistics regarding the market-wide belief
variable. From this table, we see that investors were mostly optimistic during the sample
period and that the distribution of the market-wide belief variable is left-tailed, meaning
that investors can, as suggested by Fig. 1, sometimes also become very pessimistic.
INSERT TABLE 1
C
Commonality in belief
An important assumption made in this study for developing the belief risk hypothesis is that
the movement in Zm
t is a source of commonality affecting individual stocks’ average beliefs.
To test whether there is commonality in average belief among individual stocks, we regress
changes in the average belief for each individual stock on the changes in the market-wide
belief, i.e.10
0
m
m
CZti = αi + βi,1 CZt−1
+ βi,2 CZtm + βi,3 CZt+1
+ βX Xi,t + εi,t
(6)
where CZit is, for stock i, the change from time t − 1 to t in the average belief Zit , and CZm
t
is the concurrent change in the cross-sectional average of the same variable (i.e. the marketwide belief Zm
t ). One lag and one lead of change in the market-wide belief are included to
capture any lagged adjustment in commonality. Xi,t is the set of changes in the following
variables: the growth rate in industrial production index, the growth rate in consumer price
index, the growth rate in employment, the federal funds rate, and the NBER economic
recession dummy that equals 1 when the economy is in a recession or 0 otherwise. These
10
Only stocks with as least 30 observations of Zit are considered in the examination of commonality in
belief.
16
variables are included as control variables in the regression to ensure that the covariation
in Zit , if it exists, is not driven solely by the associated macroeconomic information used
by financial analysts to forecast EPS. In each individual regression, the dependent variable
stock is excluded when computing the market-wide belief.
Cross-sectional averages of time-series slope coefficients shown in Table 2 reveal the existence of commonality in individual stocks’ average beliefs. For example, in the BR case
and when the impact of macroeconomic information is controlled for, the average value of
the estimated coefficients βi,2 ’s for the contemporaneous change in the market-wide belief is
0.737 with a t-statistic of 7.23. About two-thirds of these individual βi,2 ’s are positive while
17.84% exceeds the 5% one-tailed critical value. The average value of βi,1 ’s, although small
in magnitude, is also positive and significant. As revealed by its t-statistic, the combined
contemporaneous, lag, and lead beta coefficient, labeled ‘Sum’, is highly significant. Commonality in average belief among individual stocks is further slightly stronger in the SRWD
case.
INSERT TABLE 2
D
Belief risk factor
When forecasting quarterly EPS, besides the firm specific information contained in historical
earnings data, financial analysts may also use publicly available information about macroeconomic factors that drive variations in stocks’ earnings. If this is true, then Zm
t is not a
pure subjective belief measure and empirical results obtained with Zm
t about the pricing of
belief risk are possibly driven by the cross-sectional differences in the sensitivity of excess
stock returns to fluctuations in macroeconomic factors. As can be seen from Panel B of
17
Table 1, Zm
t is indeed strongly correlated with a set of macroeconomic variables such as the
growth rate in industrial production index, the growth rate in the consumer price index,
the growth rate in employment, the federal funds rate, and the NBER economic recession
dummy and the correlations coincide with our expectations: increases in industrial production, consumer price, employment, and the federal funds rate are accompanied by positive
market-wide belief shocks while the economic recession decreases the market-wide belief.11
Another issue preventing us from directly using Zm
t in the empirical analysis is that it is
autocorrelated and thus partially predictable. Fig. 2 plots the autocorrelation and partial
autocorrelation functions of Zm
t . In the BR (SRWD) case, the autocorrelations at the first
eight (three) lags are significantly positive.
INSERT FIGURE 2
To remove the macroeconomic and predictable components of Zm
t , we thus run the following linear regression:12
Ztm
= αz +
6
X
m
ϕi Zt−i
+ β1 IP It + β2 CP It +
i=1
β3 EM P Lt + β4 RAT Et + β5 DU Mt + εz,t
(7)
where Zm
t−i is the lagged market-wide belief in quarter t − i, IPIt is the growth rate in
industrial production index, CPIt is the growth rate in consumer price index, EMPLt is the
growth rate in employment, RATEt is the federal funds rate, DUMt is the NBER economic
recession dummy that equals 1 when the economy is in a recession or 0 otherwise, and εz,t
11
Baker and Wurgler (2006) use similar macroeconomic variables, a difference is that we also use the
federal funds rate - a factor that has been shown to strongly influence the economy.
12
The lag order is determined by fitting the time-series observations of the market-wide belief into an
autoregressive model.
18
is the normally distributed error term. In the following empirical analysis, we will rely on
the innovations in Zm
t denoted by Bt estimated from Eq. (7) as the variable of interest and
we will call this risk source belief risk.
E
Private information and biased analysts’ forecasts
Analysts’ EPS forecasts may reflect not only analysts’ subjective opinions and the public
information conveyed by historical earnings data and macroeconomic variables, but also
the private information about future EPS possessed by financial analysts. Such private
information, if it exists, will bias Zm
t as a measure of investors’ average subjective belief.
Fig. 3 plots the time series of the ratios of stocks used to construct Zm
t from each of the
ten size deciles (relative to all sample stocks). As can be seen from this figure, stocks from
the large size deciles account for a high total percentage, for instance, the ratio of stocks
from the top five size deciles exceeds 75% of the entire sample in each sample month.
INSERT FIGURE 3
The Securities and Exchange Commission (SEC) passed the Selective Disclosure and
Insider Trading Regulation on August 10, 2000, which prohibits the selective disclosure of
material non-public information by issuers to privileged individuals. This regulation, called
Regulation Fair Disclosure (FD), states that “when an issuer, or persons acting on its behalf,
discloses material non public information to certain enumerated persons (in general, securities
market professionals and holders of the issuers securities who may well trade on the basis
of the information), it must make public disclosure of that information” (SEC 2000). The
public disclosure should be made “simultaneously” for an intentional selective disclosure and
19
“promptly” for a non intentional selective disclosure by filling out Form 8-K or through any
other medium capable of mass and unbiased distribution (SEC 2000).13
The two facts discussed above should mitigate the impact of private information on
Zm
t . First, private information is much less of a concern for large-cap stocks. Second, under
regulation FD, the probability that financial analysts acts on the basis of private information
about future EPS is substantially reduced. Consequently, the private information component
m
of Zm
t should be almost negligible and Zt can be considered as a reliable measure of investors’
subjective average belief.
There is evidence in the literature that analysts issue systematically biased EPS forecasts.
De Bondt and Thaler (1985, 1987, 1990), LaPorta (1996), Dechow and Sloan (1997), Capstaff
et al. (1998), and Brown (2001) show that analysts are usually optimistic about annual and
long-term EPS forecasts, and O’Brien (1988) and Matsumoto (2002) show that analysts
become slightly pessimistic as the forecasting horizon declines. However, this empirical
analysis relies on innovations in the market-wide belief, which, by definition, are invariant
to the impact of a persistent bias in analysts’ EPS forecasts.
F
Belief risk sensitivity based stock portfolios
For each stock, we run the following regression:
ri,t − rf,t = αi + βi,m M KTt + βi,B Bt + εi,t
∀i
(8)
where ri,t is the return of stock i, rf,t is the 1-month risk-free interest rate, MKTt is the
excess market return, and Bt is the belief risk factor. The coefficient βi,B , called belief
13
Irani and Karamanou (2003) provide a detailed discussion of ‘Regulation Fair Disclosure’ and its impact
on analysts’ earnings forecasts.
20
beta, measures the sensitivity of stock i’s excess returns to innovations in the market-wide
belief (i.e., stock i’s exposure to belief risk). MKTt is included as a control variable in the
regression so that the empirical results about the pricing of belief risk obtained are not driven
by stocks’ exposures to pure stock market risk. At the beginning of each month of March,
June, September, and December during the period December 1997 through September 2009,
stocks are sorted into five equal portfolios based on their βˆB estimated with observations
in the preceding 24 quarters: stocks with βˆB in the first quintile are sorted into the first
portfolio, stocks with βˆB in the second quintile are sorted into the second portfolio, and so
forth.14 Portfolios are held for three months, and the portfolio return is calculated as the
equally-weighted average of the returns of all stocks held in the portfolio.15
V
Empirical results
In this section, we first present the main empirical results on the cross-sectional effect of
belief risk on stock returns, and then conduct various robustness tests to provide further
support on the pricing of belief risk.
A
Main results
Table 3 reports summary statistics of monthly returns delivered by the portfolios formed on
belief betas: minimum, maximum, mean, standard deviation, skewness, and kurtosis. The
14
The belief beta in Eq. (8) is estimated with the prior 24 quarters of the market belief innovations
data that are available for the time period between February 1991 and November 2009, this means that
the estimated belief beta is available starting in December 1996, the date as of which we can form stock
portfolios.
15
The results obtained with winsorized stock returns are similar, and they are available upon request.
21
returns on the highest and lowest belief beta portfolios have similar volatilities. For all the
five portfolios, the return distribution is left-skewed with heavy tails, indicating that they
suffer infrequent yet large losses.
INSERT TABLE 3
The relation between belief risk and expected stock returns is strictly positive, and portfolios composed of stocks with higher belief betas deliver higher returns. Specifically, the average return on the highest belief beta portfolio is 0.988%/month, 0.529% (i.e. 6.35%/year)
higher than the one on the lowest belief beta portfolio, and the difference is statistically
significant at the 5% level. This result provides preliminary support for the belief risk hypothesis.
A.1
Double-sorting by size and belief beta
In order to examine whether the return pattern across belief beta quintiles captures a size
effect in stock returns, we double-sort stocks based on their market capitalizations and their
belief betas. At the beginning of each month of March, June, September, and December
during the period December 1997 through September 2009, stocks are sorted into five equal
portfolios based on their market capitalizations at the end of previous month. Within each
size quintile, we run a time-series regression of excess stock returns in the preceding 24
quarters on the market factor and the belief risk factor, and stocks are then sorted into five
further equal portfolios based on their belief betas.
INSERT TABLE 4
22
The results in Panel A of Table 4 reveal that the positive relation between belief risk and
expected stock returns prevails within four out of the five size quintiles. For example, within
the fourth size quintile, the average return on the highest-minus-lowest belief beta portfolio
is 0.710%/month with a t-statistic of 2.09, and within the second and fifth size quintiles,
the average returns are respectively 0.744%/month and 0.769%/month and statistically significant at the 1% level. These results imply that size effect cannot by itself explain the
cross-sectional variations in the returns of portfolios formed on stock’s exposure to belief
risk.
It is noticeable that the cross-sectional effect of belief risk is stronger for large-cap stocks.
Within the two largest size quintiles, the average return on the highest belief beta portfolio is
over 150% higher than the one on the lowest belief beta portfolio, but the difference between
the average returns on the highest and lowest belief beta portfolios is smaller within the other
three size quintiles and even negative within the smallest size quintile. Diether et al. (2002)
find that stocks covered by financial analysts are usually issued by large firms, and Fig. 3
illustrates that the majority of stocks used to construct the market-wide belief measure have
large market capitalizations (75% of them belong to the five largest size deciles). Thus, the
market-wide belief measure constructed with the analyst EPS forecast data in this study
primarily reflects investors’ subjective belief about the earnings of large firms and will be
more relevant for the analysis of the cross-sectional effect of belief risk on the returns of
large-cap stocks. Incidentally, these stocks are also the ones that are the most prevalent
within the portfolios held by institutional investors.
23
A.2
Double-sorting by book-to-market and belief beta
We also examine whether the return pattern across belief beta quintiles captures a book-tomarket effect in stock returns by double-sorting stocks based on their book-to-market ratios
and belief betas. At the beginning of each month of March, June, September, and December
during the period December 1997 through September 2009, stocks are sorted into five equal
portfolios based on their book-to-market ratios, and within each book-to-market quintile,
stocks are sorted into five further equal portfolios based on their belief betas estimated with
observations in the preceding 24 quarters. The book value of equity is calculated as the
COMPUSTAT book value of stockholders’ equity, plus the balance sheet deferred taxes and
investment tax credit (if available), minus the book value of preferred stock. Depending on
availability, we use redemption, liquidation, or par value (in that order) to estimate the book
value of preferred stock. To ensure that the book value of equity is already known to the
market before the returns that it is used to explain, we match the book value of equity for
all fiscal years ending in calendar year y − 1 with returns starting in July of year y. The
book value of equity is then divided by the market value of equity at the end of previous
month to form the book-to-market ratio.
We observe from Panel B of Table 4 that the highest belief beta portfolio delivers a higher
average return than the lowest belief beta portfolio within all the book-to-market quintiles
and the return pattern is more pronounced for stocks with low book-to-market ratios. The
difference between the average returns on the highest and lowest belief beta portfolios exceeds
0.50%/month within the first three book-to-market quintiles and is statistically significant at
the 1% level within the second and third book-to-market quintiles. Based on these results, we
can say that the value premium puzzle is exacerbated in the presence of belief risk. Finally,
24
stocks with low book-to-market ratios usually tend to have large market capitalizations,
thus, the results in this subsection are consistent the findings in Section V.A.1.
B
Regression results
Fama and French (1996) show that sorting stocks on variables such as the book-to-market
ratio, the earnings-to-price ratio, or the cash-flow-to-price ratio can produce a strong ordering
of returns across deciles. However, they also argue that estimates of three-factor time-series
regressions indicate that the three-factor model captures these patterns in average returns.
Along these lines, we conduct similar tests to see if the return patterns observed in Tables
2 and 3 can be explained by conventional risk factors. Table 5 reports the risk-adjusted
performance (alphas) of the five portfolios formed on belief betas, evaluated with the Fama
and French (1993, FF) three-factor model, the Carhart (1997) four-factor model and the
Carhart model augmented with the Pastor and Stambaugh (2003) liquidity risk factor16 :
ri,t − rf,t = αi + βi,m M KTt + βi,s SM Bt + βi,h HM Lt + εi,t
ri,t − rf,t = αi + βi,m M KTt + βi,s SM Bt + βi,h HM Lt + βi,u U M Dt + εi,t
(9)
(10)
ri,t − rf,t = αi + βi,m M KTt + βi,s SM Bt + βi,h HM Lt + βi,u U M Dt + βi,l LIQt + εi,t (11)
where ri,t is the return of portfolio i, rf,t is the 1-month risk-free interest rate, MKTt is the
excess market return, SMBt is the excess return of small-cap stocks over large-cap stocks,
HMLt is the excess return of value stocks over growth stocks, UMDt is the excess return
of prior month winning stocks over losing stocks, LIQt is the excess return of high liquidity
beta stocks over low liquidity beta stocks, and εi,t is the normally distributed error term.
INSERT TABLE 5
16
We thank Lubos Pastor and Robert F. Stambaugh for making the data publicly available.
25
The alphas delivered by portfolios formed on the basis of their belief betas exhibit similar cross-sectional patterns as the average raw returns of those portfolios discussed so
far. For example, in the FF case, the alpha strictly increases in portfolio’s exposure to
belief risk. The lowest belief beta portfolio delivers a marginally significant negative alpha of -0.246%/month while the highest belief beta portfolio delivers a positive alpha of
0.273%/month with a t-statistic of 1.83, and the alpha of the highest-minus-lowest belief
beta portfolio is 0.519%/month and statistically significant at the 1% level, suggesting that
an investment strategy that is long in the highest belief beta portfolio and short in the lowest
belief beta portfolio will deliver a significant yearly alpha of 6.23% that cannot be explained
by the three FF risk factors. The results in Panels B and C of Table 5 suggest that the
pattern observed in the alphas cannot be explained neither by the presence of the Cahart
momentum nor of the Pastor and Stambaugh liquidity risk factors.
C
Robustness tests
The findings so far strongly support the belief risk hypothesis in that stocks with higher
exposures to belief risk earn higher expected and abnormal returns. However, it is possible
that these results are driven by model mis-specifications or alternative explanations. To
address these concerns, we next perform a series of robustness tests.
C.1
Value-weighted portfolios
While the empirical analysis in Section V.A relies on equally-weighted portfolios, we obtain
similar results for value-weighted portfolios.
INSERT TABLE 6
26
Panel A of Table 6 reports the average returns and alphas delivered by value-weighted
portfolios formed on belief beta. As documented for the case of equally-weighted portfolios,
the average return and alpha delivered by a value-weighted portfolio are increasing functions
of the exposure of this portfolio to belief risk. In fact, the difference between the (riskadjusted) returns on the highest and lowest belief beta value-weighted portfolios is even
larger and more significant. For example, the average return of an investment strategy that
is long in the highest belief beta portfolio and short in the lowest belief beta portfolio is
0.865%/month (10.38%/year) with a t-statistic of 2.79 and about 64% higher than the one
obtained with equally-weighted portfolios. This result is not surprising given that, as shown
in Panel A of Table 4 and as discussed in Section V.A.1, the cross-sectional effect of belief
risk is stronger for large-cap stocks. Finally, the positive relation between belief risk and
expected stock returns also holds within most of the size and book-to-market quintiles.
C.2
Alternative EPS forecasting model
All the results obtained above rely on the market-wide belief measure constructed with
the BR model. To understand if these results are specific to the choice of EPS forecasting
model, we conduct a similar empirical analysis, but with another market-wide belief measure
constructed with the SRWD model. Table 7 summarizes the results.
INSERT TABLE 7
Clearly, the cross-sectional effect of belief risk on stock returns remains although the difference between the average returns on the highest and lowest belief beta portfolios becomes
smaller and less significant. As discussed in Section IV.A, the SRWD model is less accurate
than the BR model in forecasting quarterly EPS, so the market-wide belief constructed with
27
the SRWD model is a biased measure of investors’ subjective opinions and the belief beta
may thus capture other factors in addition to a stock’s mere exposure to the risk arising from
stochastic fluctuations in investors’ subjective average belief. Forming portfolios based on
the noisier belief beta estimated from the SRWD model will therefore yield less significant
results. Like in the BR case, the results obtained with value-weighted portfolios are slightly
stronger.
C.3
Divergence of opinion
Diether et al. (2002) show a negative cross-sectional relationship between the divergence of
opinion among investors approximated by the dispersion in analysts’ earnings forecasts and
expected stock returns, supporting Miller’s (1977) view that divergence of opinion is priced
in the presence of short-sale constraints. Stocks with higher exposure to belief risk may also
have lower divergence of opinion so that the return pattern across belief beta quintiles is
driven by the cross-sectional effect of the divergence of opinion on stock returns. We address
this concern by double-sorting stocks into 5 × 5 portfolios based on the dispersion in analysts’
EPS forecasts scaled by the absolute value of the mean earnings forecast at the end of the
previous month and on their belief betas estimated with observations in the preceding 24
quarters. Table 8 reports average portfolio returns within each dispersion quintile. Stocks
with the zero mean earnings forecast are discarded.
INSERT TABLE 8
When looking at Table 8, we observe that the highest belief beta portfolio delivers a
significantly higher average return than the lowest belief beta portfolio within all but the
fourth dispersion quintiles. Thus, the return pattern across belief beta quintiles is clearly
28
not driven by the cross-sectional effect of the divergence of opinion. It can furthermore be
seen in Table 8 that unlike in Diether et al. (2002), there exists no clear return pattern
across dispersion quintiles, this might be due to the different data and time periods used in
this study.
C.4
Subsample analysis
Table 9 shows the results about the cross-sectional effect of belief risk on stock returns
for two separate subsample periods: the first one covers the period from December 1997
to November 2003 and the second one extends from December 2003 to November 2009.
During the first subsample period, the difference between the average returns on the highest
and lowest belief beta portfolios is 0.683%/month with a t-statistic of 1.99, and during the
second subsample period, the difference, although smaller in magnitude (0.374%/month), is
also statistically significant at the 5% level. While it remains more pronounced for largecap stocks during both subsample periods, the cross-sectional effect of belief risk varies over
time within the book-to-market quintiles: it is stronger for low book-to-market stocks during
the first subsample period but stronger for high book-to-market stocks during the second
subsample period. We further observe in Table 9 that average portfolio returns were much
higher during the first than during the second subsample period, which is due to the fact
that the second subsample period nests the 2007-09 financial crisis when stocks suffered large
losses.
INSERT TABLE 9
As discussed in Section IV.C, the Securities and Exchange Commission (SEC) passed
Regulation FD on August 10, 2000, and the regulation prohibits the selective disclosure
29
of material non public information by issuers to privileged individuals. Consequently, the
private information became a relatively less relevant issue for analysts’ EPS forecasts as of
August 10, 2000, which is prior to the beginning date of the second subsample period. If our
results were driven mainly by the cross-sectional differences in the sensitivity of stock excess
returns to fluctuations in the private information possessed by financial analysts, the crosssectional effect of belief risk should have been noticeably weaker during the second subsample
period. However, this is not what we observe and it suggests that the difference between
the average returns on the highest and lowest belief beta portfolios cannot be regarded
as compensation for the risk associated with the fluctuations in financial analysts’ private
information.
VI
A
Further discussion
Market-wide belief vs. other investor sentiment measures
A variety of investor sentiment measures have been proposed in the literature17 . In this
subsection, we discuss three well-known sentiment measures, and compare them with the
market-wide belief measure constructed in this study.
Closed-end funds are investment firms that issue a fixed number of shares traded on stock
exchanges. The closed-end fund discount is the first sentiment measure used for comparison,
and it is calculated as the difference between the net asset value of a fund’s actual security
holdings and the fund’s market price. Lee et al. (1991) argue that if closed-end funds
are disproportionately held by retail investors, the average discount on closed-end funds
17
Baker and Wurgler (2007) provide a discussion of some of these measures.
30
may represent a small investor sentiment measure, with the discount increasing when retail
investors become bearish.
Mutual fund flows were also used as a sentiment measure in previous studies such as
the ones by Brown et al. (2002) and by Ben-Rephael et al. (2012). Investors move their
money into and out of mutual funds with different levels of risk, and the changes in mutual
fund flows should reflect investors’ sentiment about market conditions. Following Baker
and Wurgler (2007), and relying on the monthly net flows data of eight equity-oriented
categories of mutual funds provided by the Investment Company Institute, we adopt the
principal component analysis approach to extract two main components from the changes in
mutual fund flows, which together can explain about 87% of variations in net flows within
the eight categories of mutual funds18 . These two principal components are used as the
second proxy for investor sentiment.
Finally, we use the Baker and Wurgler (2006) index as the third sentiment proxy. The
authors construct their composite sentiment index based on the common variation in six
underlying proxies for investor sentiment: the closed-end fund discount; the NYSE share
turnover (the ratio of reported share volume to average shares listed from the NYSE Fact
Book); the number of IPOs; the average first day returns on IPOs; the equity share in
new issues; the dividend premium (the log difference of the average market-to-book ratios
of payers and non-payers). They start by estimating the first principal component of the
six proxies and their lags. This yields a first-stage index with 12 loadings, one for each of
the current and lagged proxies. Then, they calculate the correlation between the first-stage
18
The eight equity-oriented categories of mutual funds include: “Aggressive Growth”, “Growth”, “Bal-
anced”, “Growth and Income”, “Sector”, “Income Equity”, “Income Mixed”, and “Asset Allocation”. We
thank Jeffrey Wurgler for sharing his mutual fund flows data (until May 2006) with us.
31
index and the current and lagged values of each of the proxies. Finally, they define the
sentiment index as the first principal component of the correlation matrix of six variables –
each respective proxy’s lead or lag, whichever has the higher correlation with the first-stage
index – rescaling the coefficients so that the index has unit variance.
INSERT TABLE 10
Table 10 shows that the correlations between the market-wide belief measure and all
the three sentiment measures described above are rather low. The correlation between the
closed-end fund discount and the market-wide belief measure is negative, suggesting that
the discount is low when investors are optimistic, this coincides with our expectation. The
market-wide belief measure is negatively although weakly correlated with the Baker and
Wurgler sentiment index. The graphs in the various panels of Fig. 4 further suggest that
there is no clear common pattern to be distinguished in the pairwise evolution of these
sentiment measures over time.
INSERT FIGURE 4
Although the market-wide belief measure and the above cited sentiment measures have
all been proposed to capture investors’ subjective opinions, they differ along several dimensions. First, the data used to construct these various measures are not the same. We use
analysts’ EPS forecasts to construct the market-wide belief measure while the other sentiment measures are constructed with the data on the closed-end fund discount, mutual fund
flows, share turnover, etc. Second, the underlying estimation methods are different. Third,
and most importantly, these sentiment measures capture the opinions of different categories
of investors. Baker and Wurgler (2007), Ben-Rephael et al. (2012), and Lee et al. (1991)
32
argue that their sentiment measures mainly capture the opinions of retail investors or noise
traders who, on average, are less sophisticated. As discussed in Section I, the market-wide
belief measure that we construct, by contrast, primarily represents the ave belief of institutional investors. Due to these differences, it is not surprising that the market-wide belief
measure and these other sentiment measures are only weakly correlated.
B
Understanding a stock’s exposure to belief risk
Finally, we examine how stock and firm specific characteristics affect excess stock returns’
exposures to belief risk. For this purpose, we run panel data regressions with time fixed effect
of individual belief betas on the following lagged stock and firm characteristics: the market
beta of stock returns estimated using the data over the period between 36 and 1 months
prior to t; the stock’s market capitalization in the month prior to t; the book-to-market
ratio; the accumulative return over the 11-month period between 12 and 2 months prior to
t; the annualized standard deviation of stock returns over the 12-month period between 12
and 1 months prior to t; the average stock turnover rate over the 12-month period between
12 and 1 months prior to t; the firm’s debt-to-book ratio; the firm’s sale-to-asset ratio; the
firm’s dividend-to-book ratio; the number of years between the stock’s first appearance on
the CRSP and t; and the number of financial analysts covering the stock in the month prior
to t. The accounting data from the fiscal year ending in year y −1 are matched to belief betas
from July of year y through June of year y + 1. These selected variables represent important
firm characteristics such as their size, their maturity, their leverage, their dividend policy,
their growth opportunities, and most of them were also used in the studies by Diether et
al. (2002) and by Baker and Wurgler (2006). All the regressors are standardized so that we
33
can compare their powers in explaining the cross-sectional variations of stocks’ exposures to
belief risk.
INSERT TABLE 11
Table 11 displays the regression results. The belief beta decreases with size, book-tomarket ratio, and momentum and increases with return volatility, implying that smaller,
growth, less performing and more volatile stocks face higher exposures to belief risk. The
inverse relationship between the book-to-market ratio and a stock’s belief beta suggests that
belief risk may exacerbate the well known value premium since the so far neglected exposure
to belief risk is stronger for growth stocks. Young stocks and stocks with lower analyst
coverage have higher exposures to belief risk, this result is consistent with the finding about
the relation between size and belief beta since firms issuing these stocks are usually smallsized. A high turnover rate increases a stock’s exposure to belief risk as well: frequently
traded stocks are, not surprisingly, more sensitive to innovations in investors’ average belief.
The sale-to-asset ratio has a significant positive impact on the belief beta, making these
large revenues generating firms more sensitive to belief risk regarding their future EPS.
VII
Conclusion
In this paper, we use the actual EPS and analyst EPS forecast data provided by I/B/E/S to
construct the market-wide belief measure defined as the cross-sectional average of individual
beliefs for all sample stocks, with individual belief being defined as the mean analyst EPS
forecast minus the forecast derived from an econometric EPS forecasting model. We then
test the Belief Risk Hypothesis by examining whether belief risk – the risk arising from
34
stochastic fluctuations in the market-wide belief – is priced in the cross-section of stock
returns. We find that an investment strategy that is long in stocks with high exposure to
belief risk and short in stocks with low exposure to belief risk earns an average yearly return
of 6.35%. This positive relation between belief risk and expected stock returns persists after
accounting for traditional risk factors and for portfolios double-sorted on the basis of their
size or book-to-market ratio characteristics. These results are robust to: i) an alternative
EPS forecasting model; ii) value-weighted stock portfolios; iii) accounting for divergence
of analysts’ forecasts; iv) a sub-sample analysis. Finally, we find that a stock’s exposure
to belief risk increases with its return volatility, turnover rate, and sale-to-asset ratio and
decreases with its market capitalization, book-to-market ratio, momentum, age, and analyst
coverage.
Our findings suggest that fluctuations in the average belief of investors display commonality and are a priced source of risk in stocks’ average and excess returns. Thus, our results
are closely related to Lee et al. (1991) who show that stocks and closed-end funds with high
sensitivity to investor sentiment earn an extra return as compensation for this extra risk.
The main difference between this study and Lee et al. (1991) is that we rely on a sentiment
measure expressing the average belief of a different category of investors: the market-wide
belief measure captures the average opinions of institutional investors who follow analysts’
EPS forecasts while the closed-end fund discount proposed by Lee et al. (1991) mainly captures the average opinions of retail investors. In that sense, this study complements the one
undertaken by Lee et al. (1991).
The question as to whether the risk arising from stochastic fluctuations in the average
belief (i.e. belief risk) of institutional investors – the largest category of investors active in
35
U.S. financial markets – is priced is economically relevant, but has so far not been addressed
empirically. It would be interesting in the future to examine whether belief risk is also priced
in other asset classes and in other countries. Finally, developing a theoretical model that
endogeneizes belief risk into an extended asset pricing framework seems a promising area
for future research that could shed light on its ability to rationalize some well-known asset
pricing puzzles.
36
References
[1] Anderson, W.E., Ghysels, E., Juergens, J.L., 2005. Do heterogeneous beliefs matter for
asset pricing? Review of Financial Studies 3, 875–924.
[2] Baker, M., Wurgler, J., 2006. Investor sentiment and the cross-section of stock returns.
Journal of Finance 61, 1645–1680.
[3] Baker, M., Wurgler, J., 2007. Investor sentiment in the stock market. Journal of Economic Perspectives 21, 129–151.
[4] Barone-Adesi, G., Mancini, L., Shefrin, H., 2013. A tale of two investors: estimating
optimism and overconfidence. Unpublished Research Paper No. 12-21, Swiss Finance
Institute.
[5] Basak, S., 2000. A model of dynamic equilibrium asset pricing with heterogeneous beliefs
and extraneous risk. Journal of Economic Dynamics and Control 24, 63–95.
[6] Bathke, A.W., Lorek, K.S., 1984. The relationship between time-series models and the
security market’s expectations of quarterly earnings. The Accouting Review 59, 163–
176.
[7] Ben-Rephael, A., Kandel, S., Wohl, A., 2012. Measuring investor sentiment with mutual
fund flows. Journal of Financial Economics 104, 363–382.
[8] Bradshaw, M., Sloan, R., 2002. GAAP versus the street: an empirical assessment of
two alternative definitions of earnings. Journal of Accouting Research 40, 41–66.
[9] Brown, L., 2001. A temporal analysis of earnings surprise: profits versus losses. Journal
of Accounting Research 39, 221–241.
[10] Brown, S.J., Goetzmann, W.N., Hiraki, T., Shiraishi, N., Watanabe, M., 2002. Investor
sentiment in Japanese and U.S. daily mutual fund flows. Unpublished Working Paper,
37
Yale School of Management.
[11] Brown, L., Rozeff, M., 1979. Univariate time-series models of quarterly accounting
earnings per share: a proposed model. Journal of Accounting Research 17, 179–189.
[12] Brown, N.C., Wei, K.D., Wermers, R., 2012. Analyst recommendations, mutual fund
herding, and overreaction in stock prices. Unpublished Working Paper, Georgia State
University, University of Texas - Dallas Richardson, and University of Maryland.
[13] Buraschi, A., Jiltsov, A., 2006. Model uncertainty and option markets with heterogeneous beliefs. Journal of Finance 61, 2841-2897.
[14] Carhart, M.M., 1997. On persistence in mutual fund performance. Journal of Finance
52, 57–82.
[15] Callen, J.L., Kwan, C.Y., Yip, C.Y., Yuan, Y.F., 1996. Neural network forecasting of
quarterly accounting earnings. International Journal of Forecasting 12, 475–482.
[16] Capstaff, J., Paudyal, K., Rees, W., 1998. Analysts’ forecasts of German firms’ earnings:
a comparative analysis abstract. Journal of International Financial Management and
Accounting 9, 83–116.
[17] Chen, X., Cheng, Q., 2006. Institutional holdings and analysts’ stock recommendations.
Journal of Accounting, Auditing, and Finance 21, 399–440.
[18] Ciccone, S.J., 2002. GAAP versus street earnings: making earnings look higher and
smoother. Unpublished Working Paper, University of New Hampshire.
[19] Costello, D., Hall, J., 2011. The impact of security analyst recommendations upon the
trading of mutual funds. Unpublished Working Paper, UQ Business School, University
of Queensland.
[20] Cote, D.E., Qi, R., 2005. Honest EPS: a measure of GAAP earnings relative to pro
forma earnings. International Journal of Managerial Finance 1, 25–35.
38
[21] De Bondt, W.F.M., Thaler, R., 1985. Does the stock market overreact? Journal of
Finance 40, 793–808.
[22] De Bondt, W.F.M., Thaler, R., 1987. Further evidence on investor overreaction and
stock market seasonality. Journal of Finance 42, 557–581.
[23] De Bondt, W.F.M., Thaler, R., 1990. Do security analysts overreact? American Economic Review 80, 52–57.
[24] Dechow, P., Sloan, R., 1997. Returns to contrarian investment strategies: tests of naive
expectations hypothesis. Journal of Financial Economics 41, 3–27.
[25] De Long, B., Shleifer, A., Summers, L., Waldmann, R., 1990. Noise trader risk in
financial markets. Journal of Political Economy 98, 703–738.
[26] Detemple, J., Murthy, S., 1994. Intertemporal asset pricing with heterogeneous beliefs.
Journal of Economic Theory 62, 294–320.
[27] Diether, K., Malloy, C., Scherbina, A., 2002. Differences of opinion and the cross section
of stock returns. Journal of Finance 57, 2113–2141.
[28] Doukas, J.A., Kim, C.F., Pantzalis, C., 2006. Divergence of opinion and equity returns.
Journal of Financial and Quantitative Analysis 41, 573–606.
[29] Dumas, B., Kurshev, A., Uppal, R., 2009. Equilibrium portfolio strategies in the presence of sentiment risk and excess Volatility. Journal of Finance 64, 579–629.
[30] Edelen, R.M., Warner, J.B., 2001. Aggregate price effects of institutional trading: a
study of mutual fund flow and market returns. Journal of Financial Economics 59,
195–220.
[31] Epstein, L.G., Wang, T., 1994. Intertemporal asset pricing under Knightian uncertainty.
Econometrica 62, 283–322.
[32] Fama, E.F., French, K.R., 1993. Common risk factors in the returns on stocks and
39
bonds. Journal of Financial Economics 33, 3–56.
[33] Fama, E.F., French, K.R., 1996. Multifactor explanations of asset pricing anomalies.
Journal of Finance 51, 55-84.
[34] Fang, L., Kosowski, R., 2007. Comparing stars - trading on star mutual funds’ holdings
and star analysts’ recommendations. Unpublished Working Paper, Tanaka Business
School, Imperial College London.
[35] Foster, G., 1977. Quarterly accounting data: time-series properties and predictive ability
results. The Accounting Review 52, 71–83.
[36] Franck, A., Kerl, A., 2013. Analyst forecasts and European mutual fund trading. Journal
of Banking and Finance 37, 2677–2692.
[37] Goetzmann, W.N., Massa, M., 2003. Index funds and stock market growth. Journal of
Business 76, 1–28.
[38] Griffen, P.A., 1977. The time-series behavior of quarterly earnings: preliminary evidence. Journal of Accounting Research 15, 71–83.
[39] Harris, M., Raviv, A., 1993. Differences of opinion make a horse race. Review of Financial Studies 6, 473–506.
[40] Harrison, J., Kreps, D., 1978. Speculative investor behavior in a stock market with
heterogeneous expectations. Quarterly Journal of Economics 92, 323–336.
[41] Irani, A.J., Karamanou, I., 2003. Regulation fair disclosure, analyst following, and
analyst forecast dispersion. Accounting Horizons 17, 15–29.
[42] Jouini, E., Napp, C., 2007. Consensus consumer and intertemporal asset pricing with
heterogeneous beliefs. Review of Economics Studies 74, 1149–1174.
[43] Konchitchki, Y., Lou, X., Sadka, G., Sadka, R., 2013. Expected earnings and the postearnings-announcement drift. Working Paper, University of California, Berkeley.
40
[44] Kurz, M., Motolese, M., 2011. Diverse beliefs and time variability of risk premia. Economic Theory 47, 293–335.
[45] LaPorta, R., 1996. Expectations in the cross-section of stock returns. Journal of Finance
51, 1715–1742.
[46] Lee, M.C., Shleifer, A., Thaler, R.H., 1991. Investor sentiment and the closed-end fund
puzzle. Journal of Finance 46, 75–109.
[47] Li, T., 2007. Heterogeneous beliefs, asset prices, and volatility in a pure exchange economy. Journal of Economic Dynamics and Control 31, 1697–1727.
[48] Malmendier, U., Shanthikumar, D., 2009. Do security analysts speak in two tongues.
Unpublished Working Paper, University of California, Berkeley, and Harvard University.
[49] Matsumoto, D.A., 2002. Management’s incentives to avoid negative earnings surprises.
The Accounting Review 77, 483–514.
[50] Mayshar, J., 1983. On divergence of opinion and imperfections in capital markets. American Economic Review 73, 114–128.
[51] Mehra, R., Prescott, E., 1985. The equity premium: a puzzle. Journal of Monetary
Economics 15, 145–162.
[52] Miller, E.M., 1977. Risk, uncertainty and divergence of opinion. Journal of Finance 32,
1151–1168.
[53] O’Brien, P.C., 1988. Analysts’ forecasts as earnings expectations. Journal of Accounting
and Economics 10, 53–83.
[54] O’Brien, P.C., Bhushan, R., 1990. Analyst following and institutional ownership. Journal of Accounting Research 28, 55–76.
[55] Pastor, L., Stambaugh, R.F., 2003. Liquidity risk and expected stock returns. Journal
of Political Economics 111, 642–685.
41
[56] Pavlova, A., Rigobon, R., 2007. Asset prices and exchange rates. Review of Financial
Studies 20, 1139–1180.
[57] Sadka, R., 2006. Momentum and post-earnings-announcement drift anomalies: the role
of liquidity risk. Journal of Financial Economics 80, 309–349.
[58] Schneinkman, J., Xiong, W., 2003. Overconfidence and speculative bubbles. Journal of
Political Economy 111, 1183–1219.
[59] Varian, H.R., 1985. Divergence of opinion in complete markets: a note. Journal of
Finance 40, 309–317.
[60] Williams, J.T., 1977. Capital asset prices with heterogeneous beliefs. Journal of Financial Economics 5, 219–239.
[61] Xiong, W., Yan, H., 2010. Heterogeneous expectations and bond markets. Review of
Financial Studies 23, 1433–1466.
[62] Zapatero, F., 1998. Effects of financial innovation on market volatility when beliefs are
heterogeneous. Journal of Economic Dynamics and Control 22, 597–626.
[63] Zhang, H., Zheng, L., 2011. The valuation impact of reconciling pro forma earnings to
GAAP earnings. Journal of Accounting and Economics 51, 186–202.
42
Figure 1
The top graphs plot the time series of the market-wide belief variables constructed respectively with the Brown and Rozeff (1979, BR) model and the Seasonal Random Walk with
Drift (SRWD) model, and the bottom graphs plot innovations in market-wide belief that
are estimated as the residuals of the linear regression model proposed in Section III.B. The
data covers the sample period August 1990 through August 2009.
Market Belief
−0.015
−0.002
−0.010
0.000
−0.005
0.000
0.002
0.005
0.004
Market Belief
−0.004
BR
1990
1995
2000
2005
2010
SRWD
1990
2000
2005
2010
Innovations in Market Belief
−0.002
−0.001
0.000
0.001
0.002
0.003
Innovations in Market Belief
1995
1990
1995
SRWD
−0.004
−0.003
BR
2000
2005
2010
1990
43
1995
2000
2005
2010
Figure 2
The top left graph plots the autocorrelation function (ACF) of the market-wide belief variable
constructed with the Brown and Rozeff (1979, BR) model, and the top right graph plots the
partial autocorrelation function (Partial ACF) of the same market-wide belief variable. The
bottom graphs are for the market-wide belief variable estimated with the Seasonal Random
Walk with Drift (SRWD) model.
Z_BR
0.4
0.0
−0.2
−0.2 0.0
10
15
5
10
Lag
Lag
Z_SRWD
Z_SRWD
0.8
Partial ACF
0.6
0.4
0.2
−0.4
−0.2 0.0
15
0.0 0.2 0.4 0.6 0.8
5
1.0
0
ACF
0.2
Partial ACF
0.4
0.2
ACF
0.6
0.8
0.6
1.0
Z_BR
0
5
10
15
5
44
10
15
Figure 3
This figure plots the time-series of the ratios of stocks used to construct the market-wide
belief measure from each of ten size deciles to all sample stocks. In each month for the
market-wide belief measure to be constructed, a stock is assigned to one of ten deciles based
on its market capitalization at the end of previous month. Q1 denotes the decile of the
0.6
smallest stocks and Q10 denotes the decile of the largest stocks.
0.3
0.2
0.1
0.0
Ratio
0.4
0.5
Q1
Q2
Q3
Q4
Q5
Q6
Q7
Q8
Q9
Q10
1990
1995
2000
Time Period
45
2005
2010
Figure 4
The graphs (from top left to bottom right) plot the time series of the market-wide belief
variables constructed with the Brown and Rozeff (1979, BR) model and the Seasonal Random
Walk with Drift (SRWD) model, the Backer and Wurgler (2006) sentiment index, the closedend fund discount, and the first two principal components of changes in mutual fund flows.
SRWD Market Belief
BW Sentiment Index
1.5
1.0
0.0
-1.0 -0.5
-0.015
-0.002
-0.010
0.5
0.000
-0.005
0.002
0.000
2.0
2.5
BR Market Belief
1990
1995
2000
2005
2010
1990
2000
2005
2010
2000
2005
2010
2000
2005
2010
2.0
2nd PC of Mutual Fund Flows
1.0
-0.5
0.0
0.5
-2.0 -1.5 -1.0 -0.5
1995
1995
1.5
0.5
0.0
1.5
1.0
0.5
0.0
1990
1990
1st PC of Mutual Fund Flows
1.0
Closed-End Fund Discount
1995
1990
1995
2000
46
2005
2010
1990
1995
2000
2005
2010
Table 1
Summary Statistics and Correlation Matrix
Panel A reports summary statistics of the market-wide belief variables ZBR and ZSRW D constructed with the Brown and Rozeff (1979) model and the Seasonal Random Walk with Drift
model: minimum, median, maximum, proportion of positive market-wide belief (PPMB),
standard deviation, skewness, and kurtosis. Panel B reports the correlation matrix of ZBR ,
ZSRW D , and the following macroeconomic variables: the growth rate in Industrial Production
Index (IPI); the growth rate in Consumer Price Index (CPI); the growth rate in Employment
(EMPL); the Federal Funds Rate (RATE); and the NBER economic recession dummy that
equals 1 if the economy is in a recession or 0 otherwise (DUM).
Panel A: Summary Statistics
Minimum
(%)
Median
(%)
Maximum
(%)
PPMB
(%)
Std Dev
Skewness
Kurtosis
ZBR
-0.367
0.070
0.369
74.026
0.133
-0.807
4.590
ZSRW D
-1.357
0.089
0.357
70.130
0.303
-2.808
12.321
DUM
ZBR
ZSRW D
Panel B: Market Belief and Macroeconomic Variables
IPI
CPI
EMPL
RATE
IPI
1.000
CPI
0.283
1.000
EMPL
0.895
0.318
1.000
RATE
0.531
0.490
0.612
1.000
DUM
-0.640
0.174
-0.468
-0.150
1.000
ZBR
0.559
0.285
0.495
0.297
-0.476
1.000
ZSRW D
0.823
0.478
0.659
0.384
-0.594
0.7568
47
1.000
Table 2
Market-wide Commonality in Belief
Changes in the average belief for each individual stock are regressed in time series on changes
in the market-wide belief for all stocks in the sample:
m
m
+ εi,t
+ βi,2 CZtm + βi,3 CZt+1
CZti = αi + βi,1 CZt−1
0
m
m
+ βi,2 CZtm + βi,3 CZt+1
+ βX Xi,t + εi,t
CZti = αi + βi,1 CZt−1
where ’C’ denotes a change in the variables it precedes and Xi,t is the set of changes in
macroeconomic variables used as control variables. In each individual regression, the marketwide belief excludes the dependent variable stock. Cross-sectional averages of time series
slope coefficients are reported with t-statistics in parentheses. ’Concurrent’, ’Lag’, and ’Lead’
refer, respectively, to the same, previous, and next quarter observations of the market-wide
belief. ’% positive’ reports the percentage of positive slope coefficients, while ’% + significant’
gives the percentage with t-statistics greater than +1.645 (the 5% critical level in a one-tailed
test). ’Sum’ aggregates coefficients for concurrent, previous, and next observations of the
market-wide belief. Coefficients for control variables are not reported.
BR
——————————
0.657
0.737
SRWD
——————————–
0.703
0.653
(7.14)
(7.23)
(10.16)
(8.63)
% positive
67.89
66.16
71.18
69.55
% + significant
19.67
17.84
32.79
24.85
Lag
0.242
0.280
0.158
0.106
(2.75)
(3.00)
(2.57)
(1.37)
% positive
52.19
51.89
52.24
50.81
% + significant
8.46
7.85
10.49
9.78
Lead
0.092
0.101
0.086
0.081
(1.03)
(0.99)
(1.52)
(1.35)
% positive
55.66
55.86
51.83
51.12
% + significant
9.58
9.68
11.10
9.88
Sum
0.990
1.117
0.948
0.840
(6.35)
(6.47)
(8.64)
(6.75)
Concurrent
Control Variables
Adjusted R2
Yes
0.039
0.047
48
Yes
0.072
0.087
Table 3
Summary Statistics of Monthly Portfolio Returns
This table reports summary statistics of monthly portfolio returns: minimum, maximum,
mean, standard deviation, skewness, and kurtosis. At the beginning of each month of March,
June, September, and December during the period December 1997 through September 2009,
we run a time-series regression of excess stock returns in the preceding 24 quarters on the
market factor and the belief risk factor, and stocks are sorted into five equal portfolios
based on belief beta (βB ). Portfolios are held for three months, and the portfolio return is
calculated as the equally-weighted average of the returns of all stocks in the portfolio. The
t-statistic is adjusted for autocorrelation by the Newey-West method.
βB
———————————————————————————————————–
Low
2
3
4
High
H-L
t (H-L)
Minimum
-20.72
-19.05
-17.19
-19.55
-21.75
Maximum
15.25
14.12
14.92
16.47
18.78
Mean
0.459
0.673
0.731
0.758
0.988
Std Dev
5.899
4.769
4.606
4.928
6.227
Skewness
-0.594
-0.943
-0.898
-0.911
-0.683
Kurtosis
3.836
5.281
5.433
5.717
4.634
49
0.529
2.51
Table 4
Double Sort
Panel A reports the average monthly returns of portfolios double-sorted on size and belief
beta. At the beginning of each month of March, June, September, and December during the
period December 1997 through September 2009, stocks are sorted into five equal portfolios
based on their market capitalizations at the end of previous month. Within each size quintile,
we run a time-series regression of excess stock returns in the preceding 24 quarters on the
market factor and the belief risk factor, and stocks are sorted into five further equal portfolios
based on belief beta (βB ). Similarly, Penal B reports the average monthly returns of portfolios
double-sorted on book-to-market ratio and belief beta. Portfolios are held for three months,
and the portfolio return is calculated as the equally-weighted average of the returns of all
stocks in the portfolio. The t-statistics are adjusted for autocorrelation by the Newey-West
method.
βB
———————————————————————————————————
Panel A: Double Sort on Size and Belief Beta
Size
Low
2
3
4
High
H-L
t (H-L)
Small
0.786
0.747
0.558
0.813
0.747
-0.039
-0.19
2
0.528
0.612
0.791
0.832
1.273
0.744
2.86
3
0.456
0.831
0.787
0.829
0.829
0.373
1.55
4
0.401
0.635
0.831
0.777
1.111
0.710
2.09
Large
0.199
0.447
0.647
0.643
0.968
0.769
2.81
Panel B: Double Sort on Book-to-Market Ratio and Belief Beta
B/M
Low
2
3
4
High
H-L
t (H-L)
Low
0.065
0.369
0.404
0.593
0.586
0.522
1.47
2
0.530
0.514
0.779
0.575
1.249
0.719
2.70
3
0.540
0.696
0.744
0.710
1.176
0.636
3.03
4
0.748
0.728
0.851
0.875
0.944
0.196
1.00
High
0.707
0.791
0.760
0.982
1.012
0.305
1.49
50
Table 5
Regression Results
This table reports the risk-adjusted performance (i.e. alphas) of belief beta portfolios evaluated respectively with the Fama and French (1993) model, the Carhart (1997) model, and
the Carhart model augmented with the Pastor and Stambaugh (2003) liquidity risk factor.
At the beginning of each month of March, June, September, and December during the period
December 1997 through September 2009, we run a time-series regression of excess stock returns in the preceding 24 quarters on the market factor and the belief risk factor, and stocks
are sorted into five equal portfolios based on belief beta (βB ). Portfolios are held for three
months, and the portfolio return is calculated as the equally-weighted average of the returns
of all stocks in the portfolio. The t-statistics in parentheses are adjusted for autocorrelation
by the Newey-West method.
Belief Beta Portfolios
——————————————————————————————————————
Low
2
3
4
High
H-L
——————————————————————————————————————
Panel A: Fama and French (1993) Model
α (%)
MKT
SMB
HML
R2
-0.246
(-1.65)
0.971
(29.6)
0.608
(8.77)
0.304
(5.07)
0.919
-0.023
(-0.22)
0.848
(30.7)
0.372
(5.58)
0.530
(11.0)
0.924
0.046
(0.39)
0.813
(29.2)
0.379
(5.88)
0.514
(10.6)
0.924
0.076
(0.64)
0.890
(28.6)
0.370
(4.52)
0.474
(10.4)
0.932
0.273
(1.83)
1.036
(44.4)
0.641
(11.5)
0.272
(5.66)
0.947
0.519
(2.73)
0.065
(1.90)
0.033
(0.73)
-0.032
(-0.56)
0.034
0.312
(2.28)
0.997
(26.4)
0.655
(13.2)
0.246
(5.36)
-0.066
(-3.06)
0.950
0.508
(2.38)
0.076
(1.62)
0.029
(0.67)
-0.025
(-0.38)
0.019
(0.31)
0.031
Panel B: Carhart (1997) Model
α (%)
MKT
SMB
HML
UMD
R2
-0.196
(-1.29)
0.921
(25.0)
0.626
(10.4)
0.271
(5.33)
-0.085
(-1.65)
0.926
0.025
(0.24)
0.801
(30.8)
0.390
(6.87)
0.498
(12.9)
-0.080
(-2.99)
0.933
0.092
(0.86)
0.767
(27.1)
0.395
(7.44)
0.483
(11.5)
-0.078
(-3.72)
0.934
0.115
(1.04)
0.851
(24.7)
0.384
(5.35)
0.448
(9.96)
-0.066
(-3.55)
0.938
Panel C: Carhart (1997) Model augmented with Liquidity Factor
α (%)
MKT
SMB
HML
UMD
LIQ
R2
-0.270
(-1.68)
0.914
(25.1)
0.626
(10.4)
0.276
(5.72)
-0.087
(-1.77)
0.074
(2.09)
0.928
-0.010
(-0.09)
0.798
(31.9)
0.389
(6.79)
0.501
(13.7)
-0.081
(-3.07)
0.034
(1.18)
0.934
0.026
(0.25)
0.761
(28.2)
0.395
(7.45)
0.487
(13.4)
-0.080
(-4.05)
0.066
(3.03)
0.937
51
0.059
(0.57)
0.846
(26.7)
0.384
(5.47)
0.452
(11.9)
-0.068
(-3.58)
0.057
(2.36)
0.940
0.240
(1.67)
0.990
(29.2)
0.655
(13.8)
0.251
(7.14)
-0.068
(-3.24)
0.072
(2.16)
0.952
0.510
(2.21)
0.076
(1.53)
0.029
(0.71)
-0.025
(-0.40)
0.019
(0.33)
-0.002
(-0.03)
0.024
Table 6
Value-Weighted Portfolios
Panel A reports the average monthly returns and alphas of belief beta sorted portfolios. At
the beginning of each month of March, June, September, and December during the period
December 1997 through September 2009, we run a time-series regression of excess stock
returns in the preceding 24 quarters on the market factor and the belief risk factor, and
stocks are sorted into five equal portfolios based on belief beta (βB ). Panel B (Panel C)
reports the average monthly returns of portfolios double-sorted on market capitalization
(book-to-market ratio) at the end of previous month and belief beta. Portfolios are held
for three months, and the portfolio return is calculated as the value-weighted average of the
returns of all stocks in the portfolio. The t-statistics are adjusted for autocorrelation by the
Newey-West method.
βB
————————————————————————————————————
Panel A: Sort on Belief Beta
Low
2
3
4
High
H-L
t (H-L)
Mean
0.000
0.091
0.627
0.681
0.865
0.865
2.79
FF α
-0.464
0.345
0.202
0.293
0.509
0.973
3.48
Carhart α
-0.457
-0.307
0.220
0.261
0.582
1.039
3.57
Liquidity α
-0.452
-0.232
0.160
0.229
0.479
0.931
3.12
Panel B: Double Sort on Size and Belief Beta
Size
Low
2
3
4
High
H-L
t (H-L)
Small
0.857
0.791
0.561
0.827
0.794
-0.063
-0.27
2
0.526
0.599
0.752
0.835
1.270
0.744
2.69
3
0.459
0.782
0.804
0.830
0.828
0.369
1.69
4
0.385
0.623
0.797
0.780
1.158
0.773
2.19
Large
0.107
0.050
0.544
0.697
0.687
0.580
2.12
Panel C: Double Sort on Book-to-Market Ratio and Belief Beta
B/M
Low
2
3
4
High
H-L
t (H-L)
Low
0.103
0.081
0.311
0.408
0.661
0.559
1.09
2
-0.015
0.422
0.741
0.819
1.092
1.107
3.81
3
0.069
0.170
0.870
0.828
0.804
0.735
2.01
4
0.136
0.362
1.074
0.985
1.029
0.893
2.22
High
-0.058
-0.286
0.754
0.757
1.152
1.210
2.19
52
53
Low
0.783
0.396
0.479
0.630
0.425
Low
0.121
0.603
0.757
0.902
0.792
Small
2
3
4
Large
B/M
Low
2
3
4
High
1.038
0.724
0.626
0.768
0.220
2
0.450
0.733
0.728
0.767
0.761
2
0.721
0.529
Size
2
Low
0.620
0.850
0.766
0.694
0.367
3
0.511
0.657
0.763
0.863
0.699
3
0.664
3
0.458
H-L
1.83
t (H-L)
0.252
Low
0.240
2
0.368
3
0.898
1.031
0.972
1.148
0.874
High
0.473
0.401
0.493
0.752
0.092
H-L
1.95
1.16
1.67
2.68
0.45
t (H-L)
0.360
0.599
0.448
0.368
0.884
Low
0.099
0.745
0.685
0.772
0.842
2
0.369
0.662
0.740
0.839
0.722
3
Panel B: Double-Sort on Size and Belief Beta
0.987
High
0.575
0.706
0.777
0.880
0.466
4
0.666
4
0.785
0.796
0.668
0.645
0.548
4
1.034
0.890
1.078
0.944
0.810
High
0.243
-0.012
0.321
0.340
0.689
H-L
0.90
-0.07
1.33
1.28
1.31
t (H-L)
0.087
0.345
0.443
0.424
0.270
Low
0.039
0.822
0.340
0.437
0.169
2
0.485
0.737
0.397
0.595
0.166
3
0.555
0.499
0.788
0.850
0.442
4
Panel C: Double-Sort on Book-to-Market Ratio and Belief Beta
0.625
0.699
0.773
0.873
0.535
4
0.713
4
1.131
1.207
0.998
0.752
0.777
High
0.842
1.017
1.045
1.129
0.926
High
0.887
High
1.044
0.861
0.555
0.327
0.507
H-L
0.482
0.417
0.596
0.762
0.042
H-L
0.635
H-L
2.11
2.00
1.35
0.98
0.82
t (H-L)
1.71
1.22
1.96
2.57
0.19
t (H-L)
1.86
t (H-L)
βB
————————————————————————————————————————————————————————————–
Equal-weighted Portfolios
Value-weighted Portfolios
—————————————————————————————
—————————————————————————————
Panel A: Sort on Belief Beta
in Section IV.B. The t-statistics are adjusted for autocorrelation by the Newey-West method.
belief variable and the belief risk factor are derived from using the Seasonal Random Walk with Drift model and the method proposed
return is calculated as the equally-weighted or value-weighted average of the returns of all stocks in the portfolio. The market-wide
(book-to-market-ratios) at the end of previous month and then on belief beta. Portfolios are held for three months, and the portfolio
beta (βB ). Panel B (Panel C) reports the average monthly returns of portfolios double-sorted first on their market capitalizations
preceding 24 quarters on the market factor and the belief risk factor, and stocks are sorted into five equal portfolios based on belief
and December during the period December 1997 through November 2009, we run a time-series regression of excess stock returns in the
Panel A reports the average monthly returns of belief beta portfolios. At the beginning of each month of March, June, September,
Seasonal Random Walk with Drift Model
Table 7
Table 8
Dispersion of Analyst Forecasts
At the beginning of each month of March, June, September, and December during the period
December 1997 through September 2009, stocks are sorted into five equal portfolios based on
the dispersion of analyst forecasts scaled by the absolute value of the mean analyst forecast
at the end of previous month. Within each forecast dispersion quintile, we run a time-series
regression of excess stock returns in the preceding 24 quarters on the market factor and
the belief risk factor, and stocks are sorted into five further equal portfolios based on belief
beta (βB ). Portfolios are held for three months, and the portfolio return is calculated as the
equally-weighted average of the returns of all stocks in the portfolio. This table reports the
average monthly returns of these portfolios. The t-statistics are adjusted for autocorrelation
by the Newey-West method.
Forecast
Dispersion
βB
———————————————————————————————————–
Low
2
3
4
High
H-L
t (H-L)
Small
0.917
0.914
1.014
1.039
1.688
0.772
3.20
2
0.120
0.664
0.417
0.478
0.562
0.442
2.43
3
0.281
0.384
0.674
0.685
1.077
0.797
2.71
4
0.516
0.414
0.671
0.421
0.922
0.406
1.37
Large
0.133
0.466
0.602
0.864
1.184
1.051
2.04
54
55
Low
1.278
0.940
0.799
0.556
0.323
Low
0.106
0.722
0.945
1.263
1.310
Small
2
3
4
Large
B/M
Low
2
3
4
High
1.437
1.200
0.878
0.715
0.634
2
0.640
0.840
1.132
1.044
1.325
2
1.014
0.793
Size
2
Low
1.002
1.289
1.004
0.982
0.369
3
0.759
1.153
0.883
1.160
1.038
3
0.987
3
1.338
1.325
0.982
0.682
0.946
4
0.683
H-L
1.99
t (H-L)
0.125
Low
0.332
2
0.476
3
1.359
1.351
1.254
1.872
1.267
High
1.036
0.794
0.455
0.932
-0.011
H-L
2.14
1.42
1.15
2.17
-0.03
t (H-L)
0.075
0.245
0.113
0.117
0.295
Low
0.253
0.430
0.531
0.181
0.170
2
0.535
0.510
0.692
0.422
0.077
3
Panel B: Double-Sort on Size and Belief Beta
1.476
High
0.472
0.693
0.364
0.226
0.263
4
0.450
4
1.563
1.279
1.488
1.816
1.290
High
0.253
0.016
0.543
1.095
1.184
H-L
0.65
0.05
2.07
2.55
1.83
t (H-L)
0.103
0.233
0.136
0.338
0.024
Low
0.145
0.255
0.514
0.312
0.103
2
0.517
0.412
0.483
0.576
0.440
3
0.625
0.425
0.437
0.468
0.241
4
Panel C: Double-Sort on Book-to-Market Ratio and Belief Beta
0.813
0.861
1.295
1.438
1.364
4
1.067
4
0.461
0.609
0.865
0.682
-0.117
High
0.576
0.871
0.404
0.673
0.227
High
0.499
High
0.357
0.376
0.730
0.343
-0.141
H-L
0.501
0.626
0.291
0.557
-0.068
H-L
0.374
H-L
1.96
1.78
2.20
1.31
-0.80
t (H-L)
1.79
2.21
1.39
2.00
-0.31
t (H-L)
2.16
t (H-L)
βB
————————————————————————————————————————————————————————————–
December 1997 to November 2003
December 2003 to November 2009
—————————————————————————————
—————————————————————————————
Panel A: Sort on Belief Beta
by the Newey-West method.
calculated as the equally-weighted average of the returns of all stocks in the portfolio. The t-statistics are adjusted for autocorrelation
to-market-ratios) at the end of previous month and then on belief beta. Portfolios are held for three months, and the portfolio return is
the average monthly returns during the two subsample periods of portfolios double-sorted first on their market capitalizations (book-
factor and the belief risk factor, and stocks are sorted into five equal portfolios based on belief beta (βB ). Panel B (Panel C) reports
December 2003 to November 2009, we run a time-series regression of excess stock returns in the preceding 24 quarters on the market
and December during two separate subsample periods: one extends from December 1997 to November 2003 and another extends from
Panel A reports the average monthly returns of belief beta portfolios. At the beginning of each month of March, June, September,
Subsample Analysis
Table 9
Table 10
Correlation Matrix of Market-Wide Belief and Investor Sentiment Variables
This table reports the correlations between the following variables: the market-wide belief
constructed with the Brown and Rozeff (1979) model (ZBR ) and the Seasonal Random Walk
with Drift model (ZSRW D ); the Backer and Wurgler (2006) sentiment index (SENT); the
closed-end fund discount (CEFD); and the first two principal components (PC1mf f and
PC2mf f ) of changes in mutual fund flows. The data covers the sample period August 1990
through August 2009.
ZBR
ZSRW D
SENT
CEFD
PC1mf f
ZBR
1.000
ZSRW D
0.757
1.000
SENT
-0.195
-0.130
1.000
CEFD
-0.079
-0.273
-0.203
1.000
PC1mf f
0.055
0.089
-0.199
-0.329
1.000
PC2mf f
-0.063
0.121
-0.008
0.108
-0.296
56
PC2mf f
1.000
57
# of Obs
Adj. R2 (%)
Coverage
Age
DIV/BE
Sale/AT
Leverage
Turnover
Std Dev
159,860
0.682
-1.1340∗∗∗
-0.6826∗∗∗
MoM
159,860
0.706
1.2635
∗∗∗
-0.6117∗∗∗
-0.4949∗∗∗
BE/ME
-1.0525
-1.1592
ME
159,860
0.784
2.2856∗∗∗
-1.0400∗∗∗
-0.4761∗∗∗
-1.1763
-0.8611∗∗∗
-0.6213∗∗∗
∗∗∗
3
2
∗∗∗
-0.1139
1
∗∗∗
βmkt
10% levels.
159,276
0.677
-0.0820
-0.6516∗∗∗
-0.4507∗∗∗
-1.1461
∗∗∗
-0.1154
4
159,788
0.698
0.9217∗∗∗
-0.7125∗∗∗
-0.4979∗∗∗
-1.1361
∗∗∗
-0.1134
5
159,808
0.683
-0.1252
-0.6821∗∗∗
-0.4970∗∗∗
-1.1513
∗∗∗
-0.1278
6
159,860
0.729
-1.4765∗∗∗
-0.7211∗∗∗
-0.5142∗∗∗
-0.7911
∗∗∗
-0.3149∗
7
81,613
0.578
-1.5921∗∗∗
0.1072
-0.3518∗
-0.4500∗∗
-0.2031
8
explanatory variables used in the regressions are normalized. ***, **, and * respectively denote the significance at the 1%, 5% and
data from the fiscal year ending in year y − 1 are matched to belief betas from July of year y through June of year y + 1. All the
the stock’s first appearance on CRSP and t (Age), and the number of analysts in the month prior to t (Coverage). The accounting
debt-to-book ratio (Leverage), the sale-to-asset ratio (Sale/AT), the dividend-to-book ratio (DIV/BE), the number of years between
months prior to t (Std Dev), the average stock turnover rate for the 12-month period between 12 and 1 months prior to t (Turnover), the
period between 12 and 2 months prior to t (MoM), the standard deviation of stock returns for the 12-month period between 12 and 1
the market capitalization in the month prior to t (ME), the book-to-market ratio (BE/ME), the accumulative return for the 11-month
teristics: the market beta of stock returns estimated from using the data for the period between 36 and 1 months prior to t (βmkt );
This table reports the panel data regression results with time fixed effect of individual belief betas on lagged stock and firm charac-
Determinants of Stock’s Exposure to Belief Risk
Table 11