Lesson 13: The Inscribed Angle AlternateâA
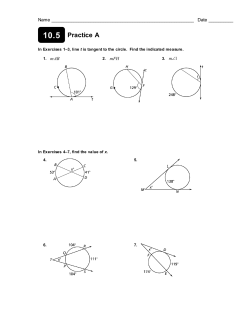
Lesson 13 M5 GEOMETRY Lesson 13: The Inscribed Angle Alternate—A Tangent Angle Classwork Opening Exercise In circle , = 56°, and is a diameter. Find the listed measure, and explain your answer. a. b. c. d. e. f. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.88 Lesson 13 M5 GEOMETRY = 56°? Explain. g. Is the h. How do you think we could determine the measure of ? Exploratory Challenge Diagram 1 Diagram 2 Examine the diagrams shown. Develop a conjecture about the relationship between and . Test your conjecture by using a protractor to measure and . Diagram 1 Diagram 2 Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.89 Lesson 13 M5 GEOMETRY Do your measurements confirm the relationship you found in your homework? If needed, revise your conjecture about the relationship between and : Now, test your conjecture further using the circle below. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.90 Lesson 13 M5 GEOMETRY Now, we will prove your conjecture, which is stated below as a theorem. THE TANGENT-SECANT THEOREM: Let be a point on a circle, let be a tangent ray to the circle, and let be a point on the circle such that is a secant to the circle. If = and is the angle measure of the arc intercepted by , then = 1 2 . Given circle with tangent , prove what we have just discovered using what you know about the properties of a circle and tangent and secant lines. a. Draw triangle . What is the measure of b. What is the measure of c. Express the measure of the remaining two angles of triangle d. What is the measure of e. Explain to your neighbor what we have just proven. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org ? Explain. ? Explain. in terms of and explain. in terms of ? Show how you got the answer. The Inscribed Angle Alternate—A Tangent Angle S.91 Lesson 13 M5 GEOMETRY Exercises Find , , , , and/or . 1. 2. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.92 Lesson 13 M5 GEOMETRY 3. 4. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.93 Lesson 13 M5 GEOMETRY 5. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.94 Lesson 13 M5 GEOMETRY Lesson Summary THEOREMS: CONJECTURE: Let circle such that be a point on a circle, let be a tangent ray to the circle, and let be a point on the is a secant to the circle. If = and b is the angle measure of the arc intercepted by , then 1 =2 . THE TANGENT-SECANT THEOREM: Let be a point on a circle, let a point on the circle such that is a secant to the circle. If the arc intercepted by , then be a tangent ray to the circle, and let be = and is the angle measure of 1 =2 . Suppose is a chord of circle , and is a tangent segment to the circle at point . If from , then = other than or in the arc of on the opposite side of is any point . Problem Set In Problems 1–9, solve for , , and/or . 1. 2. 3. 4. 5. 6. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org The Inscribed Angle Alternate—A Tangent Angle S.95 Lesson 13 M5 GEOMETRY 7. 8. 10. 9. is tangent to circle . is a diameter. Find the angle measures. is tangent to circle . is a diameter. Prove: (i) a. b. c. d. e. 11. Lesson 13: © 2014 Common Core, Inc. All rights reserved. commoncore.org = and (ii) = . The Inscribed Angle Alternate—A Tangent Angle S.96
© Copyright 2025