Investigation of Concentration Polarization and Membrane
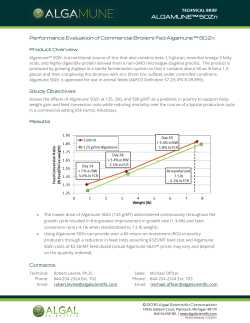
Investigation of Concentration Polarization and Membrane Permeability of a Reverse Osmosis System Chemical Engineering 104AL Group 4, Lab 1B Report 1 Rose Mina Kirkwood Jett Appel Andrew Wung Aqil Pasha Abstract The objectives of this investigation were to determine the relationship between electrical conductivity and salt concentration, estimate the membrane permeability of a Dow Filmtec SW302521 desalination membrane in a SeaRecovery Reverse Osmosis system, and examine the concentration polarization factor of the membrane surface. The concentration polarization is a phenomenon that results in a difference in the osmotic pressure between the membrane surface and the bulk feed. After acquiring data on conductivity and concentration in part one of the experiment, we plotted conductivity, in microSiemens, with respect to concentration, in moles/L, to discover that a 6 linear relationship holds between the two variables. This linear relationship is described by C(μS) = (8.95 x 10 ± 6 4 3 1.76x10)M(Mol/L) + (9.00 x 10± 2.90x10), where C is conductivity and M is concentration. To estimate the membrane permeability, we flushed deionized water through the system at different pressure drops and then calculated 12 the average permeability to be 7.987x10 ± 0.873 m/(Pas). From part two of the experiment, concentration polarization resulted in a difference between the bulk feed and membrane surface osmotic pressure. The bulk feed 4 4 4 pressure was 8.42x10 ± 0.03 Pa and the feed membrane surface osmotic pressures were 7.78x10 ± 0.08 Pa, 8.48x10 ± 4 4 4 0.06 Pa, 42.62x10 ± 0.04 Pa, 40.08x10 ± 0.07 Pa, 47.61x10 ± 0.05 Pa. The key implications of our investigation is in processes that utilize reverse osmosis, such as desalination. The main factor that must be accounted for in these processes is the effect of concentration polarization; because the osmotic pressure of the bulk feed will be different from that at the membrane surface, operators must take into account the concentration polarization effect and adjust the bulk feed pressure to achieve the desired osmotic pressure at the membrane surface. Additionally, in systems that take advantage of the conductivity of salt solutions, varying the concentrations of the solutions will proportionally vary the conductivity which can be used to optimize processes. Introduction Reverse osmosis involves the use of a semipermeable membrane to separate solutes from water. By applying a pressure that overcomes the osmotic pressure, pure water can be produced in a permeate stream. The objectives of the reverse osmosis investigation were to establish a relationship between conductivity and sodium chloride concentration, use the calculated membrane permeability value (L ) from the pure water experiment to find the osmotic pressure P difference across the membrane, and eventually find the osmotic pressure at each side of the membrane using the 3 conductivity and concentration relationship. The osmotic pressure (π) can be found using equation 1, π = ɸMRT (1) where ɸ is the Van’t Hoff Factor, M is the molarity, R is the ideal gas constant, and T is the temperature in Kelvin. (reference) Concentration can be predicted because of a positive linear relationship between concentration and conductivity . 5 The membrane permeability (L ) is found using equation 2, p J = L ΔP (2) v,water p where J is the volumetric permeate flux and ΔP is the pressure difference over the membrane. The osmotic v,water 3 pressure difference (Δπ) is found using equation 3, J = L (ΔP σΔπ) (3) v P where the reflection coefficient (σ) is assumed to equal one. The osmotic pressure at the feedside membrane surface m (π f) is found using equation 4, m Δπ = π (4) f π p 1 3 where π is the permeate osmotic pressure . A concentration gradient occurs at the membrane surface due to a p 4 phenomenon known as concentration polarization , so the osmotic pressure of the bulk feed (π ) is expected to be f different from the osmotic pressure at the membrane surface. Experimental Procedure In this experiment, we used a Dow Filmtec SW302521 seawater RO desalination membrane that has an outer 2 diameter of 2.5 inches, a length of 21 inches, and an active membrane area of 1.2 m . The maximum water feed flow rate is 0.5 gallons per minute and the maximum operating pressure is 900 psi. A simplified diagram is shown in Figure 1. Figure 1: Representation of full recycle reverse osmosis system features a tank filled to 12 liters, a pressure gauge built into the 2 reverse osmosis system to measure the pressure difference over the membrane in kg/cm , and flowmeters to measure the retentate and permeate flow in gallons per hour. The system we used was in complete recycle where the retentate and permeate streams were both returned back to the feed. The permeate is the lowsalinity product stream and the retentate is the rest of the retained solution. In part one, we developed a concentration/conductivity calibration curve by adding ten small increments of salt into a 250mL beaker full of deionized (DI) water and measuring the conductivity in microsiemens (μS) each time with a handheld conductivity meter. The amount of salt added each time was measured (on the order of 0.1 g) using an TM OHAUS Adventurer Pro AV264 balance and recorded. For part two, we first rinsed out the RO System feed tank with DI water, then filled the RO system feed tank with an NaCL solution with a concentration of 1 g NaCl/L, then recorded the conductivity of the feed solution with the handheld conductivity meter. The RO system controls were then manipulated to five different settings, and then we measured permeate flow rate, retentate flow rate, permeate conductivity, retentate conductivity, and feedside pressure. The feedside pressure could be found on the top gauge on the front of the unit. For part three, we rinsed out the RO system feed twice more with DI water to flush out any remaining salt. We then filled the tank with DI water and measured the conductivity in the DI water feed. The RO system controls were manipulated to five different settings and the following were measured: permeate flow rate, retentate flow rate, and feedside pressure. 2 Results 12 The average value for L was 7.987 x 10 ± 0.873 m/(Pas). These were calculated from pressure differences p and permeate flow rates. To observe concentration polarization, the osmotic pressure of the feed was calculated at the membrane as well as the bulk. Table 1 contains the pressure differences and osmotic pressures used to find the concentration polarization. Table 1: Data containing the change in pressure (ΔP), change in osmotic pressure (Δπ), osmotic pressure of the permeate (π ), of P m the feed at the membrane (π ), and of the bulk feed (π ) f f Concentration (mol/L) ΔP (105 Pa) Δπ (105 Pa) π P (103 Pa) m π f (105 Pa) π f (104 Pa) 0.001200 2.909 ± 0.50 0.72 ± 0.76 5.946 ± 0.01 0.778 ± 0.08 8.42 ± 0.03 0.001310 5.165 ± 0.50 0.78 ± 0.50 6.491 ± 0.01 0.848 ± 0.06 8.42 ± 0.03 0.001283 9.676 ± 0.50 4.20 ± 3.65 6.358 ± 0.01 4.262 ± 0.04 8.42 ± 0.03 0.001124 12.716 ± 0.50 3.95 ± 3.06 5.569 ± 0.01 4.008 ± 0.07 8.42 ± 0.03 0.001171 15.658 ± 0.50 4.70 ± 1.42 5.804 ± 0.01 4.761 ± 0.05 8.42 ± 0.03 Discussion Using the data collected in Part 1, Figure 4 in the appendix shows a linear relationship for concentration and 1 conductivity which agrees with theory . Any deviations could have come from errors in the machine. The introduction states that the osmotic pressure of the feed at the membrane surface is not equal to the osmotic pressure of the feed solution due to concentration polarization. Table 1 shows that the pressures at the membrane surface are, for the most m part, higher than the bulk feed osmotic pressure. Figure 2 and Figure 3 show that π fhas a positive linear relationship with feed pressure and a negative linear relationship with retentate flow respectively. Any deviations from the lines may have come from imprecise measurements of the flow rate. In part three, we calculated our average membrane permeability to be 7.987 ± 0.873 m/(Pas). The expected 2 12 permeability value for this membrane is 1.93 X 10 m/(Pas). A source of error could have come from assuming that the osmotic pressure of the permeate at the membrane surface was at one atmospheric pressure when it wasn’t. Another source of error could have come from imprecise readings of the pressure gauge. At the higher pressures, the concentration of salt could have caused the membrane pores to be blocked. This membrane fouling could have also 5 affected our data . 3 Figure 2: A membrane surface pressure vs feed pressure graph with a linear relationship between the membrane surface pressure m and the feed pressure. π is the feed pressure. f is the membrane surface pressure and P f m Figure 3: A membrane surface pressure vs retentate flow graph with a negative linear relationship. π fis the membrane surface pressure and V is the retentate flow. 4 Conclusion In the first part of this investigation we showed that there is a linear relation between the concentration of a salt solution and its electrical conductivity by measuring the conductivities of a range of salt solution concentrations. Next, in order to estimate the membrane permeability we flushed deionized water through the system under different pressure conditions and calculated the membrane permeability under each condition. The average membrane 12 permeability was then calculated to be 7.987x10 ± 0.873 m/(Pas), which is then used as an estimate for the permeability. Finally, we investigated concentration polarization by comparing the osmotic pressures at the membrane surface feed side to that of the bulk feed under various conditions. We observed that the two pressures were always different, which is expected given the concentration polarization effect. Seeing as the conductivity of solutions vary 2 1 based on the solute and the temperature of the solution , both of these factors could be investigated in future investigations. In order to investigate the effects of temperature, the conductivity of a constant concentration solution can be measured at a range of different temperatures. On the other hand, in order to investigate the effects of solute, we can measure the conductivities of different solutions of the same concentration. Additionally, more trials should be run to eliminate any possible human errors; however, in this investigation human error is minimal as the investigation relies heavily on the SeaRecovery Reverse Osmosis system. From the results of this investigation, industrial processes that utilize Reverse Osmosis can account for the concentration polarization effect to adjust the bulk feed in order to acquire the desired membrane surface feed. In addition, processes that rely on the conductivity of a solution can utilize these results to vary the concentration in order to vary the conductivity. References 1. Campbell, R. B., C. A. Bower, and L. A. Richards. "Change of Electrical Conductivity With Temperature and the Relation of Osmotic Pressure to Electrical Conductivity and Ion Concentration for Soil Extracts." Soil Science Society of America Journal 13.C, 1949, 66. Web. 2. Nobel, Park S. The BoyleVan't Hoff relation. Journal of Theoretical Biology . 1969, 23 (3), 375379 3. Harrison, R.; Todd, P.; Rudge, S.; Petrides, D. Filtration. Bioseparations Science and Engineering . New York: Oxford UP, 2003; p. 135184. 4. Porter, M. C. (1972). Concentration polarization with membrane filtration. Ind. Eng. Chem. Prod. Res. Dev ., 11, 234. 5. Hilal, N., Ogunbiyi, O. O., Miles, N. J., and Nigmatullin, R. (2005). Methods employed for control of fouling in MF and UF membranes: a comprehensive review. Sep. Sci. Tech . 2005, 40, 1957. 5 Appendix Figure 4: A concentration vs conductivity plot that shows a linear relationship where y is the concentration and x is the conductivity. To find the permeate flux, the raw data from Table 2 was used. To find the average L (membrane permeability), the p ΔP (pressure differences) and J (flux of permeate) were used. The pressure difference is calculated from the measured v pressure with the assumption of a low pressure equal to atmospheric. The permeate volumetric flux was found by 2 dividing the volumetric flow rate by the area of the membrane (1.2 m ). Table 2: Determining the average membrane permeability (L ) from pressure difference and volumetric flux (J). Includes the raw p data from measuring change in retentate flow rate as feed side pressure is varied. Distilled water was used. Permeate flow rate (GPH) Feed side press (kg/cm2 ) Pressure difference (105 Pa) J v,permeate (106 m/s) L p [1012 m/(Pas)] 3.0 ± 0.5 4.5 ± 0.5 3.4 ± 0.5 3.15 ± 0.53 9.257 ± 1.854 4.0 ± 0.5 5.0 ± 0.5 3.9 ± 0.5 4.20 ± 0.53 10.788 ± 1.729 7.0 ± 0.5 11.0 ± 0.5 9.8 ± 0.5 7.35 ± 0.53 7.517 ± 0.636 8.0 ± 0.5 14.0 ± 0.5 12.7 ± 0.5 8.40 ± 0.53 6.604 ± 0.475 10.0 ± 0.5 16.0 ± 0.5 14.7 ± 0.5 10.50 ± 0.53 7.152 ± 0.421 8.0 ± 0.5 13.0 ± 0.5 11.7 ± 0.5 8.40 ± 0.53 7.156 ± 0.525 5.5 ± 0.5 7.5 ± 0.5 6.3 ± 0.5 5.25 ± 0.53 8.274 ± 0.994 12.0 ± 0.5 19.0 ± 0.5 17.6 ± 0.5 12.60 ± 0.53 7.150 ± 0.352 Average L p 6 7.987 ± 0.873
© Copyright 2025