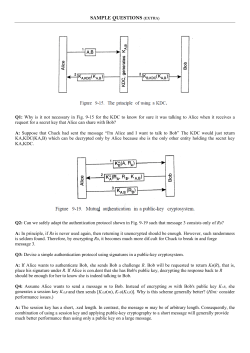
Department of Software The University of Babylon LECTURE NOTES ON Quantum Cryptography By Dr. Samaher Hussein Ali College of Information Technology, University of Babylon, Iraq Samaher@itnet.uobabylon.edu.iq 30 December 2013 Introduction • One: hard problems in mathematics – Breaking the system requires an efficient algorithm for solving a hard problem – e.g. Factoring large numbers, discrete logarithms – Examples: RSA, El Gamal – Used in public key systems – Slow • Two: information theory – Texts scrambled by repeated application of bit shifts and permutations – Examples: DES, AES – Used in private key systems – Fast 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Technology Determines What is Breakable RSA Cryptosystem C = Me mod n d = e-1 mod ((p-1) (q-1)) RSA vs. supercomputer: 40 Tflop/s (4 x 1012 flop/sec) – RSA wins! RSA vs. Quantum Computer – computer wins! 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Modern Ciphers vs. Quantum Computer • “Hard problem” variety – Exponential speedup – easily breaks algorithms such as RSA – If information requires long term protection (e.g. 20+ years), these algorithms are already dead • “Information theory” variety – Quadratic speedup (so far) – Longer keys can keep them useful 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Quantum Crypto – Why? Quantum Cryptography • is one of the new field in the cryptography to design the system promises of new level of security in the communication system • Protect against attack by quantum computer – or any future machine • Eavesdropping detection – Hard to do now • High volume key distribution – If it can be made fast enough 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Quantum Mechanics for Cryptography – Measurement Basis • Basis – frame of reference for quantum measurement • Example – polarization vertical/horizontal vs. diagonal – Horizontal filter, light gets through = 0 – Vertical filter, light gets through = 1 – 45 deg. filter, light = 0 – 135 deg. filter, light = 1 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 No cloning theorem • It is not possible to create perfect copies of a quantum state in transit for the purpose of measurement, while sending on the original. Consequently, current practical quantum cryptography setups are point to point based or at best within a Local Area Network since optical fiber amplifiers cannot be used. 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Entanglement • Two or more quantum systems can be entangled Causality and Superposition Causality, together with the superposition principle can be used for secure key distribution. If the two terms that constitute a superposition state are sent with a time delay relative to each other, and if they are not essentially connected, then Eve cannot spy on them. 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 A Quantum Key Distribution with Single Photons • The transmitter is traditionally called Alice and the receiver Bob, while the intruder is called Eve. Single photons  Quantum key distribution with single polarized photons was originally proposed by Bennett and Brassard in 1984 (BB84 protocol).  There are two data transmission channels involved: the classical (high density) and quantum (low density) channels. 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 BB84 protocol • Alice sends randomly one of the four quantum states Bit value ‘0’ 0 , 1 2 Bit value ‘1’ 1 , 1 2  0  1   0  1  • with equal probability, • When Bob receives a state from Alice, he chooses randomly either 0 , 1 , • And also Bob result correlates with the bit Alice sent only when he picked the right basis i.e. the one used by Alice. After Bob has measured the necessary number of states, Alice communicates with Bob via the classical channel and tells him when she used which basis. They discard the cases in which they used different bases, and therefore establish a secret key, called the sifted key. 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Comparing measurements Alice’s Bit 0 1 0 1 1 Alice’s Basis + × × + × Bob’s Basis + + × + × Bob’s Bit 0 0 0 1 1 Photon The test bits allow Alice and Bob to test whether the channel is secure. 30 December 2013 Dr. Samaher Hussein Ali Test bits Notes of Lecture 15 Getting the Final Key Alice’s Bit 0 1 0 1 1 Alice’s Basis + × × + × Bob’s Basis + + × + × Bob’s Bit 0 0 0 1 1 Photon Test bits discarded Final Key = 01 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 Quantum Eavesdropping • It is impossible for Eve to gain perfect knowledge of the quantum state sent by Alice to Bob. However, Eve can gain partial knowledge via a probing auxiliary quantum system in contact with the signal so that they interact, and then perform a projection measurement on the auxiliary system to retrieve some information. • Ideally we can always identify Eve by the occurrence of errors during transmission. But this is not that easy in the real world. There will always be detector noise, misalignments of detectors and transmission losses. It is not even possible in principle to distinguish errors due to noise from errors due to intrusion. We therefore have to assume that all errors are due to eavesdropping. • Since it is necessary that Alice and Bob share an identical string of bits, they must rectify any discrepancy in their sifted key. This concerns error correction and uses the public channel. 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15 QKD vs. Public/Private Key protocols 30 December 2013 Dr. Samaher Hussein Ali Notes of Lecture 15