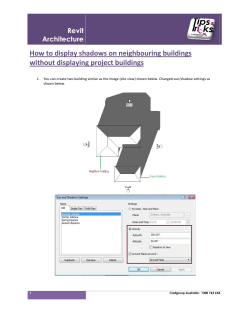
CPSC 4050 / 6050 – COMPUTER GRAPHICS SAMPLE FINAL EXAMINATION April 2014
CPSC 4050 / 6050 – COMPUTER GRAPHICS SAMPLE FINAL EXAMINATION April 2014 Name: _______________________________________ Please write all answers in the space provided following each question. Be brief and do not use extra space. Portions of the answer that exceed the allotted space will be ignored. If an equation or matrix is required as an answer, you may leave it in algebraic form (you do not have to calculate numbers or evaluate trigonometric functions). The examination is closed book and notes. The first 10 questions are “short answer” and worth 6 points each. The last 2 questions are “essay” style and worth 20 points each. 1 2 /6 3 /6 4 /6 5 /6 6 /6 7 /6 8 /6 /6 short total /60 9 10 11 12 /6 /6 /20 /20 essay total exam total /40 /100 Short-Answer Questions (6 points each). Answer all 10 of the questions in this section. 1. A CG camera is normally located in space by the position of its viewpoint, its aim direction, and an up vector. If we let pc be the viewpoint, uc be the aim direction, and vup be the up vector, give the mathematics showing how to construct the view coordinate frame ux, uy, uz of the camera. CPSC 4050 / 6050 – Sample Final Exam April 2014 2. A camera’s projection system is determined by its focal length, screen height, and screen aspect ratio (ratio of width to height). Given a camera with focal length f, screen height h, and aspect ratio a, give the screen position of 3D point x = (x, y, z), specified in the view coordinate frame of the camera. Assume a perspective projection. 3. Give a simple test to tell whether a polygon of n vertices (n > 2) is planar or not. In other words, to tell if all of the vertices lie in the same plane. 4. If a polygon is not planar, a number of different algorithms will not work correctly, for example shading calculations and ray-polygon intersection calculations, as they usually assume planarity. How would you fix this problem if the polygon were a quadrilateral? 2 CPSC 4050 / 6050 – Sample Final Exam April 2014 5. a) Give a parametric equation representing the infinite ray from a 3D point of origination pr in the direction ur (you may assume that ur is a 3D unit vector). b) Give a parametric equation representing the infinite line parallel to the direction ur and passing through the point pr. 6. Use vector equations to show how a ray-sphere intersection calculation can be done. Use an illustration to help to explain the equations. 3 CPSC 4050 / 6050 – Sample Final Exam April 2014 7. Describe algebraically the steps taken by OpenGL to do a perspective projection of a single 3D vertex x into the canonical view volume, given a modelview matrix M and a projection matrix P. You should do this in simple symbolic form. There should be no numbers or calculations. 8. Assume that the call drawcube()will draw the vertices of a 1x1x1 cube centered at the origin. The camera is located at the position (0, 0, 100), is upright and aimed down the negative z axis. Using drawcube()as the only drawing primitive, give the sequence of OpenGL calls affecting the modelview matrix needed to view a 3x4x1 box, oriented 45o to the x axis and rotated -30o with respect to its y axis, after the 45o x rotation, and finally located with its center at (5, 12, 3). 4 CPSC 4050 / 6050 – Sample Final Exam April 2014 9. Given a ray (pr, ur), and a collision data structure giving you the surface normal n, diffuse material color cd, specular material color cs, and specular exponent e, how would you compute the reflected color from the surface, given a light with color cl and direction ul towards the light. Ignore any ambient light, and assume that you have multiplication and addition defined between colors. 10. Superquadric surfaces are a family of surfaces |x/a|r + |y/b|s + |z/c|t = 1, where (x, y, z) is a 3D point in space, a, b, and c are scaling constants, and r, s, and t are exponent constants. Depending on the choice of constants a variety of shapes can be obtained, as indicated in the figure to the right. Is this representation for superquadrics a parametric or an implicit representation? Would this representation be easiest to implement for creating a polygonal surface, or for raytracing? End of Short Answer Questions 5 CPSC 4050 / 6050 – Sample Final Exam April 2014 Essay Questions (20 points each). 11. A local lighting or shading model considers only direct lighting from lights in a scene. A global lighting or shading model considers both direct light and light that is reflected between surfaces. OpenGL uses a local lighting model. The raytracing method uses a global lighting model. a) Explain why OpenGL’s model is called local and the raytracing method is called global. b) Give at least two image characteristics that “come for free” (i.e. they are intrinsic to the approach) in an image made using a global model that will only be present in an image made using a local model if special tricks or extensions are used. 6 CPSC 4050 / 6050 – Sample Final Exam April 2014 7 CPSC 4050 / 6050 – Sample Final Exam April 2014 12. Since a texture map is a fixed size image, it is often the case that a rendered pixel on the screen will be of very different resolution from the pixels in the texture map image. For example, a single screen pixel may actually cover multiple texture map pixels, when the object being projected to that pixel is far from the camera, so it is very small. Or, a single screen pixel may be much smaller than a texture map pixel when the object is close to the camera, so it is very large. Both of these situations lead to problems in the resulting texture mapped image. Explain what the artifacts will look like in both cases, and give descriptions of techniques that could be used to minimize the artifacts. 8 CPSC 4050 / 6050 – Sample Final Exam April 2014 9
© Copyright 2025