REU June 2013 Antennas Tim Pratt, Instructor
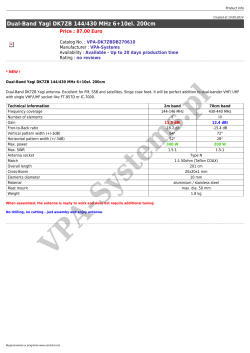
REU June 2013 Antennas Tim Pratt, Instructor tipratt@vt.edu Summer 2013 © Tim Pratt 2013 1 Topics • • • • • • • • Antenna types Antenna gain and beamwidth Antenna patterns Yagi, horns and helix Reflector antennas Phased array principles Fixed beam phased array antennas Electronically steered phased arrays Summer 2013 © Tim Pratt 2013 2 Antennas • All antennas serve several purposes • Generate controlled beam • Provide gain • Interface from waveguide or feed line to medium (air) • Antennas are often the limiting factor in a radio communication system • Definition of antenna gain: • Increase in power radiated in one direction relative to an antenna that radiates equally in all directions Summer 2013 © Tim Pratt 2013 3 Fig 10.1 Antenna Gain • Isotropic or omni-directional antenna G = 1 or 0 dB Directional antenna Axis or boresight G >> 1 Dish Summer 2013 © Tim Pratt 2013 4 Fig 10.2 Low Gain, Wide Beam Antennas • Dipole • Helix • Open ended waveguide • Small horn • Patch Summer 2013 /2 Monopole /4 Ground plane Gain 0 to 3 dB © Tim Pratt 2013 4 Cellular Handset Antennas • • • • • • • • • • Antenna must be nearly omni-directional Simplest antenna is a monopole Length is one quarter wavelength At 2000 MHz, = 0.15 m = 15 cm = 6 inches Quarter wavelength = /4 = 3.75 cm or about 1.5 ins Older cell phones had antenna on top Newer phones bury antenna inside case Ground plane is user’s hand Wider bandwidth requires a more sophisticated antenna GPS signals are at 1575 MHz – a folded F may be used Summer 2013 © Tim Pratt 2013 6 Transmission Lines • • • • • • Antennas must be fed by transmission lines Open wire pair - rarely used now, low frequencies only Coaxial line - available as rigid or flexible Impedance is set by d1, d2, dielectric constant Impedances typically 50 ohms or 75 ohms Waveguide – hollow rectangular or circular tube • Electric field in waveguide controls radiation Summer 2013 © Tim Pratt 2013 7 Fig 10.3 Rectangular Waveguide • TE 10 is the dominant mode in rectangular waveguide • Waveguide has dimensions a = 0.6 to 0.9 • b < 0.5 • E-filed is zero parallel to a conducting surface TE 10 E-field distribution b a Summer 2013 © Tim Pratt 2013 8 Fig 10.4 Circular Waveguide • TE 11 is the dominant mode in circular waveguide • Waveguide has dimensions D ~ 1 • E field must terminate normal to a conducting surface TE 11 E-field distribution Summer 2013 © Tim Pratt 2013 9 Fig 10.5 Planar Transmission Lines • Stripline and microstrip w Dielectric, t Substrate Microstrip Impedance is set by w, t, Thickness of dielectric must be controlled carefully at high microwave frequencies Summer 2013 © Tim Pratt 2013 10 Medium Gain Antennas • Higher gain can be obtained with horns and traveling wave antennas • Horns are aperture antennas • Flare out waveguide to make aperture • Field in aperture is same as in waveguide • Must be a plane wave for maximum gain • Traveling wave antennas are long – helix and Yagi Summer 2013 © Tim Pratt 2013 11 Fig 10.6 Waveguide Horn Waveguide horn with large aperture Maximum gain ~ 25 dB E field In waveguide Phase center Phase front in horn aperture is curved Summer 2013 © Tim Pratt 2013 12 Traveling Wave Antennas • • • • • • • • Yagi Helix These antennas have small aperture, medium gain Gain of Yagi antenna is approximately equal to the number of elements (not in dB) E.g. 20 elements, G ~ 13 dB Elements are spaced about / 4 Reminder: dB value = 10 log (P2 / P1) Never 20 log [ ] Summer 2013 © Tim Pratt 2013 13 Fig 10.7 Yagi (-Uda) Antenna Reflector Directors (passive) Dipole Feed line End fire array Gain is roughly equal to the number of directors (not in dB) Summer 2013 © Tim Pratt 2013 14 High Gain Antennas • In order of popularity: • Reflector with feed • Phased array • Lens with feed (rare) • Phased arrays are generally much more expensive than reflector antennas for a given gain • Phased arrays allow electronic steering of beam – used mainly in radars Summer 2013 © Tim Pratt 2013 15 Fig 10.8 Front Fed Reflector Antenna Feed pattern Waveguide horn feed Reflector (Dish) Parallel rays Edge illumination - 10 to –13 dB Summer 2013 © Tim Pratt 2013 16 Unit 2 Analysis of Antennas • • • • Gain and beamwidth Antenna patterns Examples Beam squint Summer 2013 © Tim Pratt 2013 17 Antenna Gain • Accurate formula for Gain (not in dB) • G = A 4 A / 2 = 4 Ae / 2 • A = physical area of aperture • Ae = effective area of aperture • = wavelength • A = aperture efficiency • Aperture efficiency is typically 65% in well designed antenna • For an antenna with a circular aperture diameter D • G = A ( D / ) 2 Summer 2013 © Tim Pratt 2013 18 Approximation for Antenna Gain • Approximate formula for G [empirical] • G = 33,000 / (a b) [not dB] • where a and b are antenna beamwidths in degrees in two orthogonal planes • E.g. Azimuth and Elevation • Equal beamwidths: G = 33,000 / 2 • This formula is empirical and not particularly accurate • It is useful for finding gain when beamwidths are known • Example: Satellite transmit antenna creates 3o x 4o beam • Gain is approximately 33,000 / 12 = 2750 or 34.4 dB Summer 2013 © Tim Pratt 2013 19 Fig 10.9 Creation of Antenna Pattern with an Aperture Main beam Plane wave aperture sidelobes Aperture is derived from concept in optics Same effect when a plane wave is created by an antenna Summer 2013 © Tim Pratt 2013 20 Antenna Pattern • Antenna pattern shows the distribution of transmitted power with angle for axis of beam (where gain is maximum) - see Fig 10.10 • Usually plotted in Cartesian coordinates with relative gain on vertical axis and maximum gain set to 0 dB • Beamwidth is defined between half power (-3 dB) angles • Pattern has main beam and sidelobes • Gain is highest and sidelobes largest with uniform illumination – constant field across aperture • Tapered illumination has lower field at aperture edge • Gain is lower, beam is broader and sidelobes are lower Summer 2013 © Tim Pratt 2013 21 Fig 10.10 Antenna Patterns Relative Gain dB 0 dB -3 dB Uniform illumination Tapered illumination Main beam First sidelobe -13.2 dB axis 3 dB beamwidth 0o Summer 2013 © Tim Pratt 2013 angle First null 22 Reciprocity in Antennas • Gain and Pattern of any antenna is always same for transmit and receive • We usually think of antenna pattern of transmitting antenna • Same pattern applies to antenna when receiving • Principle is called reciprocity Summer 2013 © Tim Pratt 2013 23 Rayleigh Range • Antenna requires uniform phase across aperture • Field radiates from antenna, diffracts in far field (long distance from antenna) • Forms far field pattern at R > D2 / • Pattern is constant beyond Rayleigh Range R = 2 D2 / • Beamwidth in far field is set by aperture dimension D and illumination • Typical 3 dB beamwidth for reflector antenna is 75 / D • Example: Antenna with 5 m aperture diameter at 12 GHz • = 0.025 m, 3 dB B/W = 75 x 0.025 / 5 = 0.375o Summer 2013 © Tim Pratt 2013 24 Antenna Beamwidths and Sidelobes • Beamwidth depends on aperture dimension D and illumination of aperture • Examples: • Uniform illumination = 51 D / degrees • Tapered illumination > 57 D / degrees • Depends on taper - heavier taper, wider beam • First sidelobe peak: • Uniform illumination - 13.2 dB linear, -17.6 dB circular • Tapered illumination << -13.2 dB Summer 2013 © Tim Pratt 2013 25 Antenna Example • Large antenna at 6 GHz with 30 m aperture, 65 % aperture efficiency • G = 10 log ( 0.65 x ( D / )2 ) • At 6 GHz, = 0.05 m • G = 10 log ( 0.65 x ( x 30 / 0.05)2 ) • = 10 log ( 0.65 x (1885)2 ) • = 63.6 dB • This is the upper limit for gain with a reflector antenna • Holding surface accuracy of paraboloidal dish for diameters > 30 m is difficult Summer 2013 © Tim Pratt 2013 26 Antenna Example • 3 dB Beamwidth • Typical value is 75 / D degrees • For D = 30 m, = 0.05 m • 3 dB Beamwidth = 0.125 degrees • Antenna will have to be steered to follow any signal source that moves more than 0.03 degrees, such as a GEO satellite • Typical cost: $ 5 M Summer 2013 © Tim Pratt 2013 27 Antenna Imperfections • Blockage of aperture causes null filling, higher sidelobes • Phase errors caused by surface errors also cause null filling • Asymmetric phase errors cause coma distortion • Sidelobes on one side of beam are higher than on other • Seen when feed is displaced transverse from focus of a reflector antenna • Displacing feed gives beam squint Summer 2013 © Tim Pratt 2013 28 Fig 10.11 Beam Squint with Off-axis Feed Reflector Off-axis feed Center ray Focus Summer 2013 Distorted wavefront phase © Tim Pratt 2013 29 Gain, dB Nulls filled 0 High sidelobes Coma distortion Low sidelobes 0 angle Fig 10.12 Antenna Pattern with Off-axis Feed Summer 2013 © Tim Pratt 2013 30 Reflector Antenna Configurations • Front feed: Feed blocks aperture • Offset front feed: Feed below aperture, avoids blockage • Cassegrain : Dual reflector - sub reflector inside focus of main reflector • Gregorian: Dual reflector - sub reflector outside focus of main reflector Summer 2013 © Tim Pratt 2013 31 Fig 10.13 Front Fed Reflector Antenna Feed pattern Waveguide horn feed Reflector (Dish) Parallel rays Edge illumination - 10 to –13 dB Summer 2013 © Tim Pratt 2013 32 Fig 10.14 Offset Front Fed Reflector Offset Reflector Feed pattern Parallel rays Feed This configuration is used by Directv and Dish network for direct to home satellite TV reception. The feed and LNB are below the antenna beam, avoiding blocking. Summer 2013 © Tim Pratt 2013 33 Fig 10.15 DBS-TV receive antennas Offset front fed dish Summer 2013 January 2013 © Tim Pratt 2013 34 Fig 10.16 Cassegrain Antenna Secondary Reflector (sub-reflector) Hyperboloid Feed Main Reflector Paraboloid Main reflector focus Parallel rays Cassegrain antennas are used mainly for large earth stations that need high gain antennas Summer 2013 © Tim Pratt 2013 35 Fig 10.17 Large Cassegrain antenna - fully steerable Summer 2013 © Tim Pratt 2013 36 Fig 10.18 Echostar transmit / receive station Summer 2013 ECE©4644Telecomms Tim Pratt 2013 - II Copyright Tim Pratt 2013 37 Fig 10.19 Gregorian Antenna Sub-reflector Paraboloid Feed Main reflector focus Main Reflector Paraboloid Gregorain antennas are used for mid size transportable earth stations on satellite trucks Summer 2013 © Tim Pratt 2013 38 Fig 10.20 Mobile earth station with Gregorian antenna Summer 2013 © Tim Pratt 2013 39 Reflector Antennas • Much of the development of antennas came from radar requirements • Surveillance radar needs high gain antenna • Beam scans horizon to warn of approaching aircraft, ships, missiles • Scan rate is typically 6 to 10 rpm • Tracking antenna: radar locks to target • Needs smaller antenna with high slew rate, tracking beams Summer 2013 © Tim Pratt 2013 40 Phased Arrays • Uses same aperture illumination principles as reflector antenna • Can be a fixed array or an electronically steered array • Electronic steering is used mainly in radar antennas • Beam is scanned electronically with variable phase shifters • Multiple beams are possible • Random scan possible (defeat ECM) • Nulling of jammers is possible • Complex and expensive Summer 2013 © Tim Pratt 2013 41 Radar Antennas • The ideal radar antenna is a phased array • Advantages: • Great flexibility • Multiple functions • Disadvantages: • Cost • Complexity Summer 2013 © Tim Pratt 2013 42 Fig 10.21 Planar Phased Array with Square Aperture a d Element a Aperture area = a2 Element spacing = d N elements, with N = ( a/d ) 2 Summer 2013 © Tim Pratt 2013 43 Phased Array Antennas • Phased array is made up of many active elements • Element is a dipole, helix, open ended waveguide – any small antenna with gain ~ 0 dB • Element spacing is typically d = 0.6 wavelengths • Look at number of elements needed: • For gain of G = 36 dB = 4000 = A 4 A / 2 • Assume A = 0.6 • A / 2 = 531 and a = 531 2 = 23 • For d = 0.6 N = 38 elements per side • Total number of elements in array is N 2 = 382 = 1444 Summer 2013 © Tim Pratt 2013 44 Phased Array Antennas • • • • • • • • If beamwidth = 1.4o Length of side increases to 46 Area increases to 4 x 531 2 = 2124 2 Gain increases to 36 + 6 = 42 dB N = 76 elements per side Total number of elements in the array is N2 76 x 76 = 5776 Making and driving 5776 microwave devices is expensive Summer 2013 © Tim Pratt 2013 45 Phased Array Antennas • Phased array design and cost are dominated by requirement for thousands of active elements • Useful number of elements is in range 1000 to 10,000 for array scanned in two planes • Example: 5,000 elements at $1000 each gives phased array cost of $ 5M • A reflector antenna will cost much less • Electronic scanning in one plane only reduces cost Summer 2013 © Tim Pratt 2013 46 Phased Array Antennas • High cost of an electronically steered phased array antenna can be justified when: • Antenna performs multiple functions • Antenna must have good ECCM capability • Random beam pointing is required • Rapid beam steering is required • Variable dwell time is needed • Radar has been the primary user of phased arrays Summer 2013 © Tim Pratt 2013 47 Fig 10.22 Pave Paws phased array antenna Long range VHF radar for detection of ICBMs Summer 2013 © Tim Pratt 2013 48 Fig 10.23 A/N SPY-1 phased array radar antenna Summer 2013 © Tim Pratt 2013 49 Fig 10.24 A/N SPY-1 phased array radar antenna Summer 2013 © Tim Pratt 2013 50 Fig 10.25 Phased array using slotted elements Flat panel is scanned mechanically Summer 2013 © Tim Pratt 2013 51 One Dimensional Phased Array • Simplest phased array is a linear (1-D) array • Elements are in a straight line, spaced d wavelengths apart • Element spacing d must be in range 0.5 to 1.0 wavelengths • Used to create omni directional antennas with a narrow beam in the vertical plane Summer 2013 © Tim Pratt 2013 52 Dipoles with uniform phase Broadside beam Fig 10.26 Omni directional dipole array Transmitted RF wave is vertically polarized Summer 2013 © Tim Pratt 2013 53 Phase 0o 10o Dipoles with progressive phase shift Beam is depressed to improve coverage of ground 20o 30o 40o Fig 10.27 Omni directional dipole array Transmitted RF wave is vertically polarized Summer 2013 © Tim Pratt 2013 54 Fig 10.28 Series Fed Linear Array wavefront Beam direction T wavelets dipoles T T T T load Equal time delays Summer 2013 © Tim Pratt 2013 55 Cellular Phone Base Station Antennas • Cell phone base stations use linear array antennas like the one shown in Fig 10.27. • The linear array makes a narrow beam in the horizontal plane that is tilted down a little for best coverage over the earth’s surface • Directional elements can be used to make the beam cover a sector • Cell phone towers with a large number of antennas are covering several frequency bands and providing sector coverage to increase the number of users Summer 2013 © Tim Pratt 2013 56 Fig 10.29 Cell phone tower with sector and omni antennas. Small dishes link tower to cell phone HQ and other towers. Summer 2013 © Tim Pratt 2013 57 Fig 10.30 Cell phone tower with sector antennas Summer 2013 © Tim Pratt 2013 58 Fig 10.31 Cell phone tower disguised as a tree Summer 2013 © Tim Pratt 2013 59 Fig 10.32 Parallel Fed Linear Array wavefront Beam direction T wavelets dipoles T T T T Progressive time delays Splitters Summer 2013 © Tim Pratt 2013 60 Beam Steering • Beam is steered by changing relative phase between elements • Fixed time (phase) delays give fixed beam • Cell phone tower antenna has fixed beams • Electronically controlled phase shifter gives movable beam • Used mainly in military radars because of high cost • Elements must be excited with correct amplitude distribution to control sidelobes Summer 2013 © Tim Pratt 2013 61 Beam Steering • Time delays are difficult to achieve • Phase delay is used instead • Relative phasing between elements determines beam direction • Analyze for transmit case … apply reciprocity for receive • Consider case of two adjacent elements • One element has phase shift 0o • Adjacent element has phase shift • Beam direction is to the array normal where = (2/) d sin Summer 2013 © Tim Pratt 2013 62 Fig 10.33 Setting Beam Angle Broadside Beam angle x d 0o d Summer 2013 © Tim Pratt 2013 x = d sin = (2 / ) d sin 63 Beam Steering • To form beam at angle we need progressive phase delay along array of 0o, , 2 , 3 , 4 , 5 … • Eventually N > 360o • Reset phase to N - 360o • Beam is correctly pointed only in steady state • Beam transient occurs as wavelets emerge from elements Summer 2013 © Tim Pratt 2013 64 Beam Steering • Example #1: Steer beam to 30o from normal (broadside) • Element spacing d = 0.6 • = (2 / ) d sin • = 2 x 0.6 x sin 30o • = 1.2 x ½ = 0.6 = 108o • We must insert 108o phase shift between elements Summer 2013 © Tim Pratt 2013 65 Fig 10.34 Parallel fed linear array scanned 30o Beam direction 30 degrees 108o wavefronts 0 108 216 324 Phase Shifts in degrees Splitters Summer 2013 © Tim Pratt 2013 66 Beam Steering • • • • • • Example #2: Steer beam to 45o from normal Element spacing d = 0.6 = (2 / ) d sin = 2 x 0.6 x sin 45o = 1.2 x ½ = 0.848 = 153o We must insert 153o phase shift between elements Summer 2013 © Tim Pratt 2013 67 Fig 10.35 Linear array scanned 45o Beam direction 45 degrees 153o wavefronts 0 153 306 99 Phase shifts in degrees Splitters Summer 2013 © Tim Pratt 2013 68 Conclusion • • • • • All radio transmitters and receivers need antennas Simplest antenna is a monopole or dipole Omni-directional radiation pattern, low gain Used in mobile and portable radios – e.g. cell phone Reflector and phased array antennas provide high gain and narrow beam • Used mainly for microwave links, satellite comms and radars Summer 2013 © Tim Pratt 2013 69
© Copyright 2025