Chem+14CL–Lecture+1+..
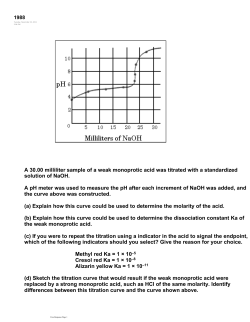
This week in lab: Tuesday/Wednesday: Check-in and Pipette calibration Thursday/Friday: Start of experiment 8: “The determination of the concentration and the acid dissociation constants of an amino acid” Experiment 8 takes a total of two lab periods (4/3-4/9) Today’s lecture: Titration of an unknown amino acids Hint: You may think of the unknown amino acid containing both HA+/- and H2A+ forms of the amino acid Definition: Polyprotic acids, also known as polybasic acids, are able to donate more than one proton per acid molecule, in contrast to monoprotic acids that only donate one proton per molecule. The protons are usually released one at a time. Examples: sulfuric acid (H2SO4=O2S(OH)2), phosphoric acid (H3PO4= (OP(OH)3), carbonic acid (H2CO3=OC(OH)2), oxalic acid ((COOH)2), all amino acids (H2N-CHR-COOH) Acid pKa1 pKa2 Ascorbic acid 4.10 11.60 Carbonic acid 6.37 10.32 Malic acid 3.40 5.20 Oxalic acid 1.27 4.27 Phthalic acid 2.98 5.28 Phosphoric acid 2.15 7.20 strong 1.92 Sulfuric acid pKa3 12.35 Amino acids are the building blocks of proteins and enzymes Amino acids have the form H2N-CHR-COOH where R is a side chain Proteins dominantly contain the (S)-enantiomer (exception: (R)-cysteine, glycine (achiral)) NutraSweet (aspartame, artificial sweetener) is a famous dipeptide composed of phenylalanine and aspartic acid Penicillins are tripeptides (L-Cysteine, D-Valine, L-Aminoadipic acid) The isoelectric point is the pH value at which the molecule carries no net electrical charge (HL). At this point, the amino acid displays its lowest solubility in polar solvents (i.e., water, salt solutions) and does not migrate in the electrical field either. H H H N S O N O CH3 CH3 COO-K+ Diprotic acids undergo the following equilibria: H2L+ HL HL + H+ L- + H+ Ka1 Ka2 Three possible forms in solution: H2L+, HL, L The solution contains all three species at any given time. The individual concentration depends on the pH-value. Example: Bicarbonate buffer system pH<6.37: [H2CO3] > [HCO3-] >>> [CO32-] pH=6.37: [H2CO3]=[HCO3-] 6.37<pH<8.35: [HCO3-] > [H2CO3] >> [CO32-] 8.35<pH<10.32: [HCO3-] > [CO32-] >> [H2CO3] pH=10.32: [HCO3-]=[CO32-] pH>10.32: [CO32-] > [HCO3-] >>> [H2CO3] Relevance: pH-value of blood: 7.35-7.45 pH=7.4: 91.5% HCO3-/8.5 % H2CO3 H2CO3 H2CO3 Leucine pKa1=2.33 pKa2=9.75 Since Ka1 >>> Ka2, only the first equilibrium has to be considered at low pH-values What is the pH-value of a 0.05 M H2L+ solution? x2 Ka1 = [0.05 x] The 5 % rule fails in this case. Thus, the quadratic formula has to be used here. x =1.31 * 10-2 M = [H+] (=26.2 %>>5 %) pH= -log([H+])=1.88 For the calculation above, we assumed that the second equilibrium was unimportant (L- ≈ 0). However, using the number above we can find the true concentration. [H ][L ] Ka2 = [HL] Ka2[HL] -10 = 1.79x10 L- = [H ] With [HL] = [H+] =1.31 * 10-2 M. The calculation shows that the concentration of L- is indeed very low compared to the other concentrations. Titration of diprotic acid has six points of interest P1: Initial pH-value P2: pH-value at halfway to first equivalence point (pH=pKa1) P3: pH-value at first equivalence point P4: pH-value at halfway to second equivalence point (pH=pKa2) P5: pH-value at first equivalence point P6: pH-value after adding excess of base V= 0 Veq/2 Veq 1.5 Veq 2 Veq 2.5 Veq Example: Titration of 10 mL of 0.050 M H2L+ with 0.050 M NaOH Two reactions have to be considered H2L+ + OHHL + H2O (1) HL + OHL- + H2O (2) Step 1: Initial pH-value (see previous calculation) Step 2: After 5.0 mL of base have been added, [H2L+]=[HL] pH=pKa1=2.33 Step 3: After 10.0 mL of base were added, the first equivalence point is reached (=isoelectric point) pK a1 pK a 2 2.33 9.75 pH 2 2 pH=6.04 Step 4: After 15.0 mL of base have been added, [HL]=[L-] pH=pKa2= 9.75 Step 5: After 20.0 mL of base were added, the second equivalence point is reached. Since all of HL is converted to L-, the hydrolysis of L- has to be considered (ICE). L- + H2O HL + OH- LInitial Change Equilibrium 5.0*10-4 moles (=0.010 L *0.050 M) -x (5.0 * 10 4 x ) 0.030L HL OH- ~0 ~0 +x +x x y 0.030L x y 0.030L Step 5 (continued): Determine pKb of L- Determine [OH-] K w 1.0 *10 14 5 Kb 5 . 59 * 10 K a 1.79 *10 10 Kb y2 [ L ] y Using the quadratic equation, one obtains y = [OH-] = 9.38*10-4 M (= 5.5 % of 0.0167 M) pOH = 3.03 pH=10.97 Step 6: After 25.0 mL of base have been added, all H2L+ has been converted to L-. This required 20.0 mL of base to accomplish. There is an excess of 5.0 mL of base in the solution Find number of moles of base n = 0.0050 L * 0.050 M = 2.5*10-4 moles Find concentration of base c = 2.5*10-4 moles/0.0350 L = 7.14*10-3 M Find pOH and pH pOH = -log([OH-]) = 2.15 pH = 14 – pOH = 11.85 The six points of interest in the titration of 0.050 M leucine with 0.050 M NaOH are Point Base added Equivalence pH-value Comments P1 0.0 mL 0.0 1.88 P2 5.0 mL 0.5 2.33 =pKa1 P3 10.0 mL 1.0 6.04 =(pKa1+pKa2)/2 P4 15.0 mL 1.5 9.75 =pKa2 P5 20.0 mL 2.0 10.97 P6 25.0 mL 2.5 11.85 In lab, this week on Thursday and Friday The student obtains a standardized NaOH solution. The students have used pH meters before (Chem 14BL) so the calibration should go rather smoothly. If you do not remember how to do it anymore, please review it in the lab manual (page 12). Make sure to keep the standardized sodium hydroxide and the unknown amino acid solution. DO NOT store your standard solution (NaOH) in volumetric flasks. Use other glassware to store the solutions (ask your TA). The student has to perform three titrations of the unknown amino acid solution (until pH=12) Clean-up Neutralize all titrant solutions with citric acid until the pH paper turns light green or orange before discarding in the drain. Pour the small amount of waste NaOH used to rinse the burette into the labeled waste container. Do not pour un-neutralized NaOH solutions down the drain. At the end of the assignment, place the capped bottles of unused NaOH and amino acid on the lab cart for return to the lab support Use Excel for plotting titration curves and first-derivative graphs. The pKa’s of the amino acid are determined from the full titration graph To determine pKa1 and pKa2, locate the volume on the graphs half way between the two equivalence point volumes determined from the expanded derivative curves. The pH at this point is in the titration is equal to pKa2. Next, measure an equal distance on the graph to the left of Vep1. The pH at this point is equal to pKa1. Error Analysis: Calculate the relative average deviation in the concentrations of your amino acid. Compare the relative average deviation with the inherent error calculated by propagating the errors in measurements of the pipet, the volumes determined from the graphs, and the standard base solution. Estimate the absolute error in your pKa’s by considering the variability you had in the pH’s of the solutions at the |DVep/2| points in the three titrations. Report the range for each of the pKa’s. The report is due on April 15, 2014 or April 16, 2014 at the beginning of the lab section.
© Copyright 2025