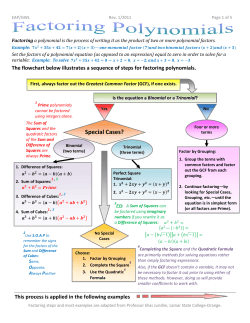
Document 97866
Factoring Patterns
5-7 Factoring Pattern for x 2 + bx + c,
c positive
Objective
To factor quadratic trinomials whose quadratic coefficient is 1
and whose constant term is positive.
In this lesson you will study trinomials that can be factored as
a product of the form (x + r)(x + s), where r and s are both
positive or both negative. The diagram shows that the product
(x + r)(x + s) and the trinomial x2 + (r + s)x + rs represent the
same total area. Notice that the coefficient of the x-term is the
sum of r and s, and the constant term is the product of r and s.
Example 1 (x + 3)(x + 5) = x2 + 8x + 15
sum of 3 and 5
I
T
product of 3 and 5
Example 2 (x — 6)(x – 4) = x2 – 10x+ 24
sum of –6 and –4-1
product of –6 and –4
The examples above suggest the following method for factoring trinomials
whose quadratic coefficient is 1 and whose constant term is positive.
1. List the pairs of factors whose products equal the constant term.
2. Find the pair of factors in the list whose sum equals the coefficient of the
linear term.
Examples 1 and 2 suggest that in Step 1 you need to consider only the factors
with the same sign as the linear term.
Example 3 Factor y2 + 14y + 40.
Solution
1. Since the coefficient of the linear term
is positive, list the pairs of positive
factors of 40.
2. Find the factors whose sum is 14: 4 and 10.
3.
y2 + 14y + 40 = (y + 4)(y + 10)
Answer
Factors
of 40
1
2
4
5
Sum of the
factors
40
20
10
8
Factoring Polynomials
41
22
14
13
213
Example 4 Factor y2 — 11y + 18.
Solution
1. Since —11 is negative, think of the negative factors of 18.
2. Select the factors of 18 with sum —11: —2 and —9
3. .•. y2 — 1 ly + 18 = (y — 2)(y — 9) Answer
A polynomial that cannot be expressed as a product of polynomials of
lower degree is said to be irreducible. An irreducible polynomial with integral
coefficients whose greatest monomial factor is 1 is a prime polynomial.
Example 5 Factor x2 — 10x + 14.
Solution
1. The pairs of negative factors of 14 are: —1, —14; —2, —7.
2. Neither of these pairs has the sum —10.
3.
x2 — 10x + 14 cannot be factored. It is a prime polynomial.
Answer
Oral Exercises
The area of each rectangle is represented by the trinomial below it. Use the
diagram to factor the trinomial. You may wish to make models from grid
paper, using a 10-by-10 square for x2, a 10-by-1 rectangle for x and a
1-by-1 square for 1.
x
Sample
6
Solution
x2
x
12
12
x2 + 8x + 12 = (x + ?)(x + ?)
9
1.
.v
x2 + 8x + 12 = (x + 2)(x + 6)
2.
3.
?x
9.A-
4
x2 + 5x + 4 =
(x + ?)(x + ?)
8
Chapter 5
x2
?x-
12
x 2 + 6x + 8 =
(x + ?)(x + ?)
214
x
x2 + 7x + 12 =
(x + ?)(x + ?)
Find two integers with the given sum and product.
Example
4. 5.
6.
7.
8.
9.
10.
11.
12.
13.
Sum
5=4+1
5
7
-6
-6
8
10
-9
-11
-10
12
Product
4=4-1
6
6
8
9
15
16
18
24
24
32
For each trinomial tell which two factors of the constant term have a sum
equal to the coefficient of the linear term.
Sample
x2 - 13x + 22
Solution
(-2)(-11) = 22 and -2 + (-11) = -13
-2 and -11 are the correct factors. Answer
14. x2 + 8x + 7
17. y2 + 7y + 12
20. r2 + 9r + 20
23. y2 + 25y + 24
15.
18.
21.
24.
z2 - 6z + 5
c2 - 15c + 14
s2 - 12s + 20
x2 + 1 lx + 28
16.
19.
22.
25.
p2 - Sp + 6
u2 + llu + 18
x2 - 14x + 24
n2 - 17n + 30
Written Exercises
Factor. Check by multiplying the factors. If the polynomial is not
factorable, write prime.
A
1. x2 + 5x + 4
4. c2 - 10c + 16
7. q2 16q + 15
10. s2 - 12s + 40
13. u2 + 12u + 28
16. 64 - 20s + s2
3. r2 - 6r + 8
6. p2 - 14p + 13
9. a2 - 15a + 26
12. z2 + 16z + 39
15. 42 - 23k + k2
18. 75 + 27u + u2
2. z2 + 9z + 8
5. y2 - 9y + 14
8. n2 + 10n + 21
11. x2 + 20x + 36
14. x2 - 22x + 72
17. 75 + 20r + r2
Sample
x2 - 10xy
Solution
x2 - 10xy + 21y2 = (x - ?)(x - ?)
= (x - 3y)(x - 7y)
21y2
Check: (x - 3y)(x - 7y) = x 2 - 3xy - 7.xy + 21y2
= x2 - 10xy + 21y2
19. p2 + 19pq + 34q2
22. x2 - 15xy + 72y2
20. a2 + 10ab + 24b2
23. u2 - 50uv + 49v2
25. x2 - 16xy + 45y2
28. p2 + 20pq + 50q2
26. m2 + 20mn + 51n2
21. c2 - 16cd + 48d2
24. h2 - 14hk + 49k2
27. a2 + 17ab + 52b2
29. r2 - 15rs + 54s2
30. a2 - 12ab + 27b2
Factoring Polynomials
215
Factor. Check by multiplying the factors.
B 31. y2 + 20yz + 91z2
34. 108 - 24y + y2
32. w2 + 20wm + 96m2
35. 112a2 - 22ab + b2
33. 124 - 35y + y2
36. 117x2 - 22xy + y2
Find all the integral values of k for which the trinomial can be factored.
Sample
x2 + kx + 28
Solution
28 can be factored as a product
of two integers in these ways:
(1)(28) (-1)(-28)
(2)(14) (-2)(-14)
(4)(7) (-4)(-7)
The corresponding values of k are
29, 16, 11, -29, -16, and -11. Answer
37. y2 + ky + 14
40. p2 + kp + 18
38. x2 + kx + 10
41. n2 + kn + 9
39. z2 + kz + 12
42. r2 + kr + 20
Find all positive integral values of k for which the trinomial can be
factored.
43. n2 + 6n + k
44. z2 + 7z + k
46. x2 + 9x + k
45. y2 + 8y + k
Factor completely.
C 47.
(y + 2) 2 - 6(y + 2) + 5
49. (y + 3) 2 + 6(y + 3) + 9
51. x4 - 5x2 + 4
48. (t + 3)2 + 8(t + 3) + 15
50. z6 - 17z4 + 16z2
52. r4 - 29r2 + 100
54. (a - 4)2 + 5(a - 4)(a + 2) + 6(a + 2)2
53. t5 - 20t3 + 64t
55. Factor a2n 30anb2n 209b4n, where n is a positive integer.
56. Factor p4" - 30p2nqn + 221q2n, where n is a positive integer.
Mixed Review Exercises
Solve.
1. -13 + x = -9
4. n + 2 =13 - 61
2. d + (-5) = -6
5. 19m = 76
3. -15 + b = 8
6. 3p + 18 = -72
7. - 1x= 12
8. -r3- - 4 = 5
9. -21x = 252
Simplify.
10. (5y + '7)(5y - 7)
216
Chapter 5
11. (2xy 3)3
12. (2x2)6
5-8 Factoring Pattern for x 2 + bx + c,
c negative
Objective
To factor quadratic trinomials whose quadratic coefficient is 1
and whose constant term is negative.
The factoring that you did in the last lesson had this pattern:
x2 + bx + c = (x + r)(x +
T
T
c positive
r and s are both positive or both negative.
The factoring that you will do in this lesson has the following pattern:
x2 + bx + c = (x + r)(x + s)
T
T r and s have opposite signs.
c negative
T
When you find the product (x + r)(x + s), you obtain
x2 + bx + c = x2 + (r + s)x + rs
Therefore, the method used in this lesson is the same as before. You find two
numbers, r and s, whose product is c and whose sum is b. Since c is negative,
one of r and s must be negative and the other must be positive.
Example 1 Factor x2 — x
Solution
—
20.
1. List the factors of —20 by writing them
down or reviewing them mentally.
2. Find the pair of factors with sum —1:
4 and —5.
3. ... x2 — x — 20 = (x + 4)(x — 5) Answer
You can check the result by multiplying
(x + 4) and (x — 5).
Factors
of —20
1
—1
2
—2
4
—4
Sum of the
factors
—20
20
—10
10
—5
5
—19
19
—8
8
—1
1
Example 2 Factor a2 + 29a — 30.
Solution
1. The factoring pattern is (a + ?)(a — ?).
2. Find the pair of factors of —30 with sum 29: 30 and —1.
3. .•. a2 + 29a — 30 = (a + 30)(a — 1) Answer
Example 3 Factor x2 4kx — 12k2 .
Solution
1. The factoring pattern is (x + ?)(x — ?).
2. Find the pair of factors of —12k 2 with a sum of —4k: 2k and —6k.
3.
x2 — 4kx — 12k2 = (x + 2k)(x — 6k) Answer
Factoring Polynomials
217
Oral Exercises
Find two integers with the given sum and product.
Example
Sum
1 = 3 + (-2)
Product
-6 = 3(-2)
5.
4.
8.
7.
6.
9.
10.
2.
3.
2
-3
-2
15
3
-7
1
0
2
-10
-3
-10
-15
-16
-18
-18
-30
-25
-24
-24
1.
For each trinomial tell which two factors of the constant term have a sum
equal to the coefficient of the linear term.
Sample
X2 -
Solution
(-7)(4) = -28 and -7 + 4 = -3
-7 and 4 are the correct factors.
3x - 28
11. z2 + 3z - 4
14. p2 + p - 12
17. x2 + 2x - 15
Answer
12. z2 - 4z - 5
15. y2 - 5y - 14
18. u2 - u 2
13. c2 - c - 6
16. r2 - 2r - 8
19. k2 + 8k - 9
-
■
111•11
11111111111W
Written Exercises
Factor. Check by multiplying the factors. If the polynomial is not
factorable, write prime.
A
1. y2 + 5y - 6
4. x2 + 2x - 8
7. n2 + 2n - 6
10. p2 + 7p 18
13. x2 - 25x - 54
16. z2 + z - 72
19. u2 + 9uv - 70v2
22. m2 + mn - 56n2
-
3. x2 - 6x - 16
6. u2 - 10u - 9
9. b2 - 13b - 30
12. y2 - 4y - 32
15.
- 21y - 72
18. r2 - 2Ors - 44s 2
14. t2 - 16t - 40
17. a2 - ab - 42b2
21. h2 - 25hk 54k2
24. a2 - 13ab - 48b2
20. x2 - 2xy - 63y2
23. p2 - 16pq - 36q2
.
-
Sample
1 - iox - 24x2
Solution
Find two factors of -24x 2 whose sum is -10x: 2x and -12x.
1 - 10x - 24x2 = (1 + 2x)(1 - 12x) Answer
B 25. 1 - 2n - 48n2
27. x2 - 10xy - 75y 2
218
2. v2 - 3v - 4
5. c2 - 4c - 12
8. a2 - 5a - 24 11. y2 + 12y - 36
Chapter 5
26. 1 + 15c - 34c2
28. a2 + 5ab 84b2
-
30. 1 - 15mn - 100m 2n2
32. n2 + 9n - 400
29. 1 + llpq - 80p2q2
31. p2 + 2p - 360
33. -380 + x + x2
34. -800 - 20a + a 2
Find all the integral values of k for which the given polynomial can be
factored.
35. y2 + ky - 28
36. c2 + kc - 20
38. x2 + kx - 36
37. p= + kp - 35
Find two negative values of k for which the given polynomial can be
factored. (There may be many possible values.)
39. r2 - 2r + k
42. k - 7r + r2
41. k + 5x + x2
44. k - 6z + z 2
40. y2 + 4y + k
43. k + 4t + t2
Factor completely.
C 45.
46. t4 - 7t2 - 18
48. (x + 2) 2 - 4(x + 2) - 21
50. (p + q)2 - 2(p + q) - 15
52. (p + q)2 - 2r(p + q) - 15r2
54. (a + b)4 - (a - b)4
x4 - 3x2 - 4
47. x4 - 15x2y2 - 16y4
49. (y + 3) 2 + 5(y + 3) - 24
51. (a + b)2 - (a + b) - 2
53. (a + b)2 - c(a + b) - 2c2
55. Factor x2n - 4Xny2n 221y4n, where n is a positive integer.
4x2nyn - 252y2n, where n is a positive integer.
56. Factor x4'
Mixed Review Exercises
Simplify.
1. (9x2y)(3xy2)(2x2)
4. (3x - 4)2
5 00
0 6
10(xy)3
10. (n + 3p)2
7.
2. (3x - 4)(2x + 3)
5 . (7x.sy2)3
3. -7x(3x2 - 2x + 4)
6. 5y(2y2 + 3y + 5)
8.
0. (-n)6
-4ab
-12ab3
11. (a - 6)(5a + 2)
_ nio
12. (2y + 7)2
Factor.
13. 15m - 21n + 9
16. a2 - 13ab + 42b2
19. u2 - 10u + 25
22. 49w4 - 16x2
25. 9x2 - 24xy + 16y2
28. a2 + 13a - 68
14.
17.
20.
23.
26.
121k2 - 81
16x2 + 24x
44 + 15y + y2
4m2 + 20m + 24
56 - 15z + z2
29. 25w6 - 144x6
15.
18.
21.
24.
27.
a2 + 18a + 81
64 - n2
7a2b3 - 14ab
c2 - 11c - 26
x2 - 1
30. 25a2 + 20ab + 4b2
Factoring Polynomials
219
5-9 Factoring Pattern for ax e + bx + c
Objective
To factor general quadratic trinomials with integral coefficients.
If axe + bx + c (a> 1) can be factored, the factorization will have the pattern
(px + r)(qx + s).
Example 1 Factor 2x2 + 7x — 9.
Solution
Clue 1 Because the trinomial has a negative constant term, one of r and s will be
negative and the other will be positive.
Clue 2 You can list the possible
factors of the quadratic term,
2x2, and the possible factors
of the constant term, —9.
Test the possibilities to see
which produces the correct
linear term, 7x. Making a
chart will help you do this.
Since (2x + 9)(x — 1) gives
the correct linear term,
2x2 + 7x — 9 = (2x + 9)(x — 1).
Answer
Factors of 2x2
2x, x
Factors of —9
1, —9 —1, 9
3, —3 —3, 3
9, —1 —9, 1
Possible factors
Linear term
(2x + 1)(x — 9) (-18 + 1)x = —17x
(2x + 3)(x — 3)
(-6 + 3)x = —3x
(2x + 9)(x — 1)
(-2 + 9)x = 7x
(2x — 1)(x + 9)
(18 — 1)x = 17x
(2x — 3)(x + 3)
(6 — 3)x = 3x
(2x — 9)(x + 1)
(2 — 9)x = —7x
Example 2 Factor 14x2 — 17x + 5.
Solution
Clue 1 Because the trinomial has a positive c onstant term and a negative linear term,
both r and s will be negative.
Clue 2 List the factors of the quadratic
term, 14x2 , and the negative
factors of the constant term, 5.
Test the possibilities to see
which produces the correct
linear term, —17x.
Since (2x — 1)(7x — 5) gives
the correct linear term,
14x2 — 17x + 5 = (2x — 1)(7x — 5).
Answer
220
Chapter 5
Factors of 14x2
x, 14x
2x, 7x
Possible factors
(x — 1)(14x — 5)
(x — 5)(14x — 1)
(2x — 1)(7x — 5)
(2x — 5)(7x — 1)
Factors of 5
—1, —5
—5, —1
Linear term
(-5 — 14)x = —19x
(-1 — 70)x = —71x
(-10 — 7)x = —17x
(-2 — 35)x = —37x
Remember to check each factorization by multiplying the factors. After
some practice you will be able to select the correct factors without writing
down all the possibilities.
When the coefficient of the quadratic term is negative, it may be helpful to
begin by factoring —1 from each term.
Example 3 Factor 10 + llx — 6x2 .
I Arrange the terms by
Idecreasing degree.
10 + 1 lx — 6x2 = —6x2 + 1 lx + 10
{ Factor —1 from each term.
= ( —1)(6x2 — 1 lx — 10)
{ Factor the resulting trinomial.
= (-1)(2x — 5)(3x + 2)
= —(2x — 5)(3x + 2) Answer
Note: If you factor 10 + l lx — 6x2 directly, you will get (5 — 2x)(2 + 3x).
Since (5 — 2x) = —(2x — 5), the two answers are equivalent.
Solution
Example 4 Factor 5a 2 — ab — 22b2 .
Solution
{Write the factors of 5a 2 .
)
)(5a
{ Test possibilities.
= (a + ?)(5a — ?)
= (a + 2b)(5a — 11b) Answer
If you write (a — ?)(5a + ?) as the second step, you will not find a
combination of factors that produces the desired linear term.
5a2 — ab — 22b2 = (a
Note:
Oral Exercises
The area of the rectangle is represented by the trinomial below. Use the
diagram to factor the trinomial.
Sample
Solution
4x'
6.v
2x
3
4x2 + 8x + 3
4.v2
1
2.v
4x2 + 8x + 3 =(2x+3)(2x+ 1)
1.
3 v=
3x
3x2 + 5x + 2
2x
6x=
4x
3x
6x2 + 7x + 2
Factoring Polynomials
221
For each quadratic trinomial tell whether its factorization will have the form
(px + r)(qx + s),
(px + r)(qx - s),
or (px - r)(qx - s),
where p, q, r, and s represent positive integers.
3. 2x2 + x - 6
6. 4x2 - 4x - 3
9. 3x2 + 4x - 4
12. 9x2 + 6x - 8
4. 5x2 - 13x + 6
7. 2x2 - x - 10
5. 4x2 + 8x + 3
8. 6x2 + 5x + 1
11. 8x2 - 25x + 3
14. 10x2 - 10x - 9
10. 5x2 - 1 lx + 2
13. 14x2 + 13x + 3
Written Exercises
Factor. Check by multiplying the factors. If the polynomial is not
factorable, write prime.
A 1. 3x2 + 7x + 2
3. 3c2 - 8c + 5
5. 5y2 + 4y - 1
7. 5u2 - 6u - 2
9. 7x2 + 8x + 1
5x2 - 17x + 6
3. 3p2 + 7p - 6
15. 4y2 - y - 3
4. 2x2 - 15x + 7
6. 3a2 + 4a - 4
8. 3r2 - 2r - 5
10. 2p2 + 7p + 3
12. 7m2 - 9m + 2
14. 4c2 + 4c - 3
16. 6a2 - 5a - 2
5 + 7x - 6x2
9. 1 - 5b - 8b2
21. 3m2 + 1 lmn + 6n2
18. 9 + 6k - 8k2
20. 7 - 12s - 4s2
22. 2p2 - 7pq + 6q2
23. 2x2 + xy - 3y2
24. 5a2 - 2ab - 7b2
B 25. 9m2 - 25mn - 6n2
27. 6r2 - 1 lrp + 5p2
29. 21c2 + 4c - 12
31. 6 + 7a - 20a2
26.
28.
30.
32.
33. 32n2 - 4n - 15
35. 21c2 + 22c - 24
34. 33u2 - u - 14
36. 35y2 + 2y - 24
C 37.
2(a + 2)2 + 5(a + 2) - 3
39. 2(a + 2b) 2 + 5(a + 2b)c - 3c2
41. 4x4 - 17x2 + 4
43. (y2 + 3y - 1)2 - 9
222
2. 2x2 + 5x + 3
Chapter 5
6h2 + 17hk + 10k2
4x2 + 16xy - 9y2
18z2 + 19z - 12
8 + 45r - 18r2
38. 2(x - 1)2 - 9(x - 1) - 5
40. 2(x - y)2 - 9(x - y)z - 5z2
42. 2x4 - 15x2 - 27
44. (a2 - 4a - 1)2 - 16
45. Show that (15x2 — 14x + 3)(6x2 + 19x — 7)(10x2 + 29x — 21) is a perfect
square by showing that it is the square of a polynomial.
46. Factor 90a8'1+1b2 25,24n+t b2n+2 _ 240ab 4n+2, where n is a positive
integer.
Mixed Review Exercises
Factor.
1. x2 — 225
4. c2 — 6c + 9
7. y2 + 15y + 56
10. m2 — m — 72
2. x2 — 9x + 20
5. 9y2 — 289x2
8. p2 + 12p + 36
11. n2 + 15n + 36
3. r2 — 5r — 14
6. 4a4 — 49
9. 16y2 + 24y + 9
12. b2 — 2b — 24
Self-Test 3
Vocabulary irreducible polynomial (p. 214)
prime polynomial (p. 214)
Factor.
1. a2 + 12a + 35
3. n2 — 3n — 28
5. 2r2 — 7r + 6
Obj. 5-7, p. 213
2. x2 — 10x + 16
4. c2 + 3cd — 40d2
Obj. 5-8, p. 217
6. 3x2 + 10xy — 8y2
Obj. 5-9, p. 220
■
MIA I I VA I I I /Mil/AMP/AM I I/AM I VA INIAI
Challenge
According to the legend, the inventor of the game of chess asked to be rewarded by
having one grain of wheat put on the first square of a chessboard, two grains on the
second, four grains on the third, eight grains
on the fourth, and so on. The total number
of grains would be 264 — 1, which is several
thousand times the world's annual wheat yield.
1. To find how large 264 is approximately,
you could enter the number 2 on the
calculator and press the squaring button
a number of times. How many times must
you press this button?
2. Factor 264 — 1 as a difference of squares to
show that it is divisible by 3, 5, and 17.
Factoring Polynomials
223
General Factoring and Its
Application
5-10 Factoring by Grouping
Objective
To factor a polynomial by grouping terms.
A key tool in factoring polynomials is the distributive property:
ba + ca = (b +c)a
This property is valid not only when a represents a monomial, but also when a
represents any polynomial. For example:
If a = x + 2, you have
b(x + 2) + c(x + 2) = (b + c)(x + 2)
If a = 3r — s + 7, you have
b(3r — s + 7) + c(3r — s + 7) = (b + c)(3r — s + 7)
Example 1 Factor:
a. 5(x + y) + w(x + y)
b. m(m + 4n) — (m + 4n)
Solution
a. (5 + w)(x +
b. (m — 1)(m + 4n)
Another helpful tool is recognizing factors that are opposites of each other.
Factor
x—y
4 — a2
2n — 3k — 1
Opposite
—(x — y)
—(4 — a2)
—(2n — 3k — 1)
or
or
or
—x + y
—4 + a2
—2n + 3k + 1
or y — x
or a2 — 4
or 3k — 2n + 1
Example 2 Factor 5(a — 3) — 2a(3 — a).
Solution
Notice that a — 3 and 3 — a are opposites.
5(a — 3) — 2a(3 — a) = 5(a — 3) — 2a[—(a — 3)]
= 5(a — 3) + 2a(a — 3)
= (5 + 2a)(a — 3) Answer
In Example 3 you first group terms with common factors, and then factor.
Example 3 Factor 2ab — 6ac + 3b — 9c.
Solution 1 2ab — 6ac + 3b — 9c = (2ab — 6ac) + (3b — 9c)
= 2a(b — 3c) + 3(b — 3c)
= (2a + 3)(b — 3c) Answer
224
Chapter 5
Solution 2 2ab — 6ac + 3b — 9c = (2ab + 3b) — (6ac + 9c)
= b(2a + 3) — 3c(2a + 3)
= (b — 3c)(2a + 3) Answer
Example 4 uses what you know about factoring perfect square trinomials
and differences of squares.
Example 4 Factor 4p2 — 4q2 + 4qr — r2 .
Solution
A trinomial square
4p2 — 4q2 + 4qr — r2 = 4p2 — (4q2 — 4qr + r2)
The difference of two squares.
<
= (2p) 2 — (2q
= [2p + (2q — r)][2p — (2q — r)]
= (2p + 2q — r)(2p — 2q + r) Answer
In Example 4 you could have tried the grouping (4p 2 — 4q2) + (4qr — r2)
and factored the groups to obtain 4(p + q)(p — q) + r(4q — r). But this doesn't
lead anywhere. There are different approaches to factoring a polynomial. You
may need to try several before arriving at one that works.
Oral Exercises
Factor.
1. a(a — 2) + 3(a — 2)
4. x(x + 2y) — (x + 2y)
7. x(x — 4) — (4 — x)
2. p(q + 1) — 4(q + 1)
5. u(u + v) — v(u + v)
8. m(n — m) — n(m — n)
3. 2r(r — 3) — 5(r — 3)
6. h(h — 2) + 2(2 — h)
9. 2r(r — s) + s(s — r)
Written Exercises
Factor. Check by multiplying the factors.
A 1. 3(x + y) + z(x + y)
3. e(f — g) — 4(f — g)
5. 7(r — s) + t(s — r)
7. 2a(a + 3) — (3 + a)
9. 2x(x — y) + y(y — x)
11. 2u(u — 2v) + v(u — 2v) + (u — 2v)
2. 7(r — s) + t(r — s)
4. w(x — y) — 8(x — y)
6. 7(m — n) + p(n — m)
8. u(v — 2) + 2(2 — v)
10. 3p(2q — p) — 2q(p — 2q)
12. a(a — b) + 4b(a — b) — a(a — b)
13. x(2w — 3v + u) — (2w — 3v + u)
15. (s2 — 2ps + 2s) — (2s — 4p + 4)
14. r(r — s — 2t) + s(r — s — 2t)
16. (x2 — xy + x) — (y — x — 1)
17. (3t — 3st) + (rs — r)
18. (9p — 3pq) + (2nq — 6n)
19. (12x2 — 8xy) — 5(3xz — 2yz)
20. (p2 — 2pq) — 2(2qr — pr)
Factoring Polynomials
225
Factor. Check by multiplying the factors.
21. 3a + ab + 3c + bc
23. x2 - 2x + xy - 2y
25. h2 - hk + hr - kr
22. rs + 5r + st + 5t
24. u2 - 2u + uv - 2v
27. p3 - 2p2 + 4p - 8
29. p2 - 2pq + pr - 2qr
31. 3hk - 2k - 12h + 8
33. 4z3 - 6z2 - 6z + 9
35. (h2k2 + 4k2) + (h2k + 4k)
37. x3 - 3x2 - x + 3
28. 3a3 + a2 + 6a + 2
30. u2 - 3uv - 6uw + 18vw
32. 3ab - b - 4 + 12a
34. 3u3 - u2 - 9u + 3
36. (a2b2 + 2a2) - (2ab2 + 4a)
38. n 3 + 2n2 - 4n - 8
26. x2 - 2xy + 4xz - 8yz
Factor each expression as a difference of squares.
40. (a + 2b)2 - 9c2
39. x2 - (y - z) 2
41. (u - 2v)2 - 4w2
42. 4p2 - (q - 2r)2
B 43.
44. 4(x + y) 2 - (2y - z) 2
46. x2 - 2xy + y2 - 4
(a + 2b)2 - (2b + c)2
45. a2 + 4a + 4 - b2
47. u2 - v2 + 2v - 1
49. h2 - 4k2 - 4h + 4
51. p 2 a2 r.2 _ 2pr
48. m2 - n2 - 2m + 1
50. a2 - b2 - 2a + 1
52. 4s2 - 4t2 + 4s + 1
Factor.
53. x2 - 4y2 + 4z2 - 4xz
55. a2 + b2 + 2ab + 2a + 2b
54. m2 - 9n2 + 9 - 6m
56. p2 - q2 - 2p + 2q
57. x4 - y4 - 4x2 + 4
59. p2 + q2 - r2 - 2pq + 2r - 1
58. a4 + b4 - c4 + 2a2b2
60. h2 - 4k2 + 4h - 8k
C 61.
Factor x4 + 4 by writing it as (x4 + 4x2 + 4) - 4x2 , a difference of two squares.
62. Use the method of Exercise 61 to factor (a) 64x4 + 1 and (b) x4 + 4a4.
63. Factor a2n± 1 b2"+1 a2nb2n + a to. where n is a positive integer.
Mixed Review Exercises
Solve.
1. -12 + x = -29
4. 16 = 1 + 3z
7. 14x -= 700
10. 10n = 2n - 24
226
Chapter 5
2. -n + 10 = 2
5. 10m - 6m = 36
8. -13n = 156
11. 19m = 55 + 14m
3. 18 + x = 32
6. 5n - 2n + 8 = 9
9. 9b = 108
12. lOy + 6 = 4(19 - y)
5-11 Using Several Methods of Factoring
Objective
To factor polynomials completely.
A polynomial is factored completely when it is expressed as the product of a
monomial and one or more prime polynomials
1. Factor out the greatest monomial factor first.
2. Look for a difference of squares.
3. Look for a perfect square trinomial.
4. If a trinomial is not a square, look for a pair of binomial factors.
5. If a polynomial has four or more terms, look for a way to group the terms
in pairs or in a group of three terms that is a perfect square trinomial.
6. Make sure that each binomial or trinomial factor is prime.
7. Check your work by multiplying the factors.
Example 1 Factor —4n4 + 40n3 — 100n2 completely.
Solution
—4n4 + 40n3 — 100n2 = —4n2(n2 — 10n + 25)
perfect square trinomial
greatest monomial factor
= —4n2(n — 5) 2 Answer
Example 2 Factor 5a3b2 3a4b — 2a2b3 completely.
Solution
First rewrite the polynomial in order of decreasing degree in a.
5a3b2 3a4b — 2a2b3 = 3a4b 5a3b2 — 2a2b3
= a2b(3a2 + 5ab — 2b2)
trinomial
greatest monomial factor --I
= a2b(3a — b)(a + 2b) Answer
Example 3 Factor a2bc — 4bc + a2b — 4b completely.
Solution
a2bc — 4bc + a2b — 4b = b(a2c — 4c + a2 — 4)
= b[c(a2 — 4) + (a2 — 4)] {Factor by grouping.
= b(c + 1)(a 2 4) < Difference of squares
= b(c + 1)(a + 2)(a — 2)
Answer
Factoring Polynomials
227
Oral Exercises
State the greatest monomial factor of each polynomial.
1. 6a2 - 9ab - 15b2
2b - 15a3b4.6ab+9
3. 15r3 + 20r2s - 20rs2
6. 12x2y - 36xy2 + 27y3
2. 18x - 8x3
5. 4(z - 4)2 - 16
Factor completely.
7. 10a2 - 15ab2
4 + 6y3 + 9y2
10.y
8. -4x + 6x2
11. p3 - 2p2q + pq2
9. t3 - 9f
12. u3v - uv3
Written Exercises
Factor completely.
A
1-6. The polynomials in Oral Exercises 1-6.
7. 5a2 + 10ab + 5b2
9. 4m3 - m
11. y4 - 2y2 - y3
10. 3xy 2 - 27x3
12. -n4 - 3n2 - 2n3
13. x2 - xy - x + y
- 14.
15. -41a + 10 + 21a2
17. a3 - 2a2b + 3a2 - 6ab
19. 6U2V 11U2V2 10U2v3
21. k(k + 1)(k + 2) - 3k(k + 1)
23. 2u5 - 7u3 - 4u
16. 80 - 120p + 45p2
-m2 + mn + 2m - 2n
25. r2 - 6r - 9s2 + 9
27. u2 - 4v2 + 3u - 6v
8p3q - 18pq3
180x2y - 108xy2 - 75x3
n(n2 - 1) + n(n - 1)
81a + 18a3 + a5
26. x2 - 4y2 - 4x + 4
28. a2 - b2 + ac - bc
29. p2 - 1 - 4q2 - 4q
30. x2 - 2x - 4y2 - 4y
B 31.
100 + 4x2 - 16y2 - 40x
33. a4 - b4
35. 2pq + 2pr + q2 - r2
37. (a + b)2 - (a - c)2
39. x3 x2y xy2 + y3
41. a(a + 2)(a - 3) - 8(a - 3)
43. 16c 16 - 16
45. a(a2 - 9) - 2(a + 3)2
47. 9u2 - 9v2 - 36w2 + 36vw
228
8. 6c2 + 18cd + 12d2
Chapter 5
18.
20.
22.
24.
32. 16x2 + 16y - y2 - 64
34. m8 - n8
36. 8a3 + 4a2b - 2ab2 - b3
38. 3x5 + 15x3 - 108x
40. 4 - 4x2 - 4y2 + 8xy
42. x(x + 1)(x - 4) + 4(x + 1)
44. (u - v) 3 + v - u
46. (x - 2)(x2 - 1) - 6x - 6
48. x4 - x2 + 4x - 4
C 49.
x2(x + 2) — x(x + 2) — 12(x + 2)
51. et — 10t2 + 9
50. (a + b)3 — 6(a + b)2 — 7(a + b)
52. 16/4 — 8t2 + 1
53. a2 + b2 — c 2 — d2 — 2ab + 2cd
54. (u2 — v2)2 — w2(u + v)2
55. Factor x4 + x2 + 1 by writing it as (x4 + 2x2 + 1) — x2 , a difference of squares.
56. Factor a4 a2b2 + b4 . (Hint: See Exercise 55.)
57. Factor a3 + b3 by writing it as a 3 alb — a2b — ab2 + ab2 + b3 and
grouping the terms by pairs.
58. Factor a3 — b3 . (Hint: See Exercise 57.)
.
Mixed Review Exercises
Simplify.
1. (-1)4)(40)
2. 1(56)
8
4. 140b
5. 52 + (*)
3. 91 (72) ( )
6. 625 + (-5)
Factor.
7. x2 — 12x + 35
8. x2 + 3x — 28
10. 2n2 + 19n + 9
11. 3x2 + llx + 10
9. x2 — x — 2
12. (3x -- 12) — 2n(4 — x)
Career Note / Draftsperson
Manufacturers and construction workers
rely on detailed plans of buildings and
manufactured products as a guide for
production. The plans are prepared by a
draftsperson using many different tools.
For example, he or she may use a
compass, a protractor, a triangle, and a
calculator. A draftsperson also makes use
of math skills, such as working with
fractions, making measurements, and
making drawings to different scales.
Today draftspersons use computeraided design (CAD) systems to allow
them to see many variations of a design.
They often specialize in a particular field
of work, such as mechanical, electrical,
aeronautical, or architectural drafting. A
draftsperson needs coursework in mathematics, mechanical drawing, and drafting.
Factoring Polynomials
229
5-12 Solving Equations by Factoring
Objective
To use factoring in solving polynomial equations.
The multiplicative property of zero can be stated as follows:
If a = 0 or b = 0, then ab = 0.
statement
The statement above is given in "if-then" form. The converse of a statement
in "if-then" form is obtained by interchanging the "if" and "then" parts of
the statement as shown below.
If ab = 0, then a = 0 or b = 0. <— converse
The converse of a true statement is not necessarily true. You can show that
the particular converse displayed above is true (Exercise 55, page 233).
The words "if and only if" are used to combine a statement and its converse when both are true. The zero-product property stated below combines the
multiplicative property of zero and its converse.
Zero-Product Property
For all real numbers a and 12:
ab = 0 if and only if a = 0 or b = 0.
A product of factors is zero if and only if one or more of the factors is zero.
The zero-product property is true for any number of factors. You can use this
property to solve certain equations.
Example 1 Solve (x + 2)(x — 5) = 0.
Solution
One of the factors on the left side must equal zero. Therefore,
x + 2 = 0 or x — 5 = 0
x = —2
x=5
Just by looking at the original equation, you might have seen
that when x = —2 or x = 5 one of the factors will be zero.
Either method gives the solution set {-2, 5}.
Example 2 Solve 5n(n — 3)(n — 4) = 0.
Solution
5n = 0 or n — 3 = 0 or
n=3
n=0
the solution set is {0, 3, 4}.
230
Chapter 5
n— 4 = 0
n=4
Answer
Answer
A polynomial equation is an equation whose sides are both polynomials.
Polynomial equations usually are named by the term of highest degree. If
a 0 0:
ax + b = 0 is a linear equation.
axe + bx + c = 0 is a quadratic equation.
ax3 + bx2 + cx + d = 0 is a cubic equation.
Many polynomial equations can be solved by factoring and then using the
zero-product property. Often the first step is to transform the equation into
standard form in which one side is zero. The other side should be a simplified
polynomial arranged in order of decreasing degree of the variable.
Example 3 Solve the quadratic equation 2x 2 + 5x = 12.
Solution
1. Transform the equation into standard form.
2. Factor the left side.
2x2 + 5x — 12 = 0
(2x — 3)(x + 4) = 0
3. Set each factor equal to 0 and solve.
2x — 3 = 0 or x + 4 = 0
2x = 3
x = —4
x= 3
4. Check the solutions in the original equation.
4-
2()
2
+
54) 1 12
2(-4)2 + 5(-4) 1 12
1 12
2(16) — 20 1 12
2(4) +
2++
—
24 = 12 ,/
.*. the solution set is {-}, —4}.
32 — 20 = 12
Answer
Example 4 Solve the cubic equation 18y 3 + 8y + 24y2 = 0.
Solution
1. Transform the equation into standard form.
2. Factor completely.
3. Solve by inspection or by equating each
factor to 0.
4. The check is left to you.
.*. the solution set is {0, —1}.
18y3 + 24y2 + 8y = 0
2y(9y2 + 12y + 4) = 0
2y(3y + 2)2 = 0
y = 0 or y =
2
Or y =
2
Answer
The factorization in Example 4 produced two identical factors. Since the factor
3y + 2 occurs twice in the factored form of the equation,
is a double or
multiple root. Notice that we list it only once in the solution set.
Factoring Polynomials
231
Caution: Never transform an equation by dividing by an expression containing a variable.
Notice that in Example 4, the solution 0 would have been lost if both sides of
2y(9y2 + 12y + 4) = 0 had been divided by 2y.
Oral Exercises
Solve.
1. x(x - 6) = 0
4. (y -- 2)(y + 3) = 0
2. 2a(a + 1) = 0
5. 0 = (3t - 2)(t - 3)
3. 0 = 3p(2p - 1)
6. x(2x - 5)(2x + 1) = 0
Explain how you could solve the given equation. Then solve.
8. a3 = 4a
11. 9x2 = x3
7. 4x2 - x3 = 0
10. m3 - 2m = m2
9. k2 + 4 = 4k
12. 0 = - n3 + n
13. Give an example of a true "if-then" statement with a false converse.
Written Exercises
Solve.
A 1. (y + 5)(y - 7) = 0
4. 2x(x - 20) = 0
7. 3x(2x + 1)(2x + 5) = 0
10. p2 - p - 6 = 0
13. m2 - 36 = 16m
16. x2 = 20x - 100
19. 4x2 - 9 = 0
22. 3x2 + x = 2
25. 7x2 = 18x - 11
28. 10u3 - 5u2 = 0
31. 8y2 - 9y + 1 = 0
34. 25x2 - 90x = -81
B 37. 4x3 - 12x2 + 8x = 0
40. 9x3 + 25x = 30x2
Sample 1
Solution
232
2. (n + 1)(n + 9) = 0
5. (2t - 3)(3t - 2) = 0
8. n(5n - 2)(2n + 5) = 0
11. 0 = x2 + 14x + 48
14. r2 + 9 = lOr
17. y2 = 16y
20. 25m2 - 16 = 0
23. 4s - 4s2 = 1
26. 2y2 = 25y + 13
29. 0 = 4y3 - 2y2
32. 6h2 + 17h + 12 = 0
35. 4p2 + 121 = 44p
38. 2n3 - 30n2 + 100n = 0
41. y4 - 10y2 + 9 = 0
3. 15n(n + 15) = 0
6. (2u + 7)(3u - 1) = 0
9. y2 - 3y + 2 = 0
12. 0 = k2 - 12k + 35
15. s2 = 4s + 32
18. 9k2 = 4k
21. 6n2 + n = 2
24. r - 6r2 = -1
27. 8u3 - 2u2 = 0
30. 0 = 10x3 - 15x2
33. 15u2 - 14u = 49
36. 6c2 - 72 = llc
39. 9x3 + 9x = 30x2
42. u5 - 13u3 + 36u = 0
(x - 1)(x + 3) = 12
"
x2 1- -
Chapter 5
3 - 12 = 0
(x - 3)(x + 5) = 0
the solution set is {3, -5}
Solve. See Sample 1 on page 232.
= 16
43. (z + 1)(z — 5)
44. (2t — 5)(t
— 1) = 2
45. (x — 2)(x + 3) = 6
46. (a — 5)(a — 2) = 28
47. x(x — 6) = 4(x — 4)
48. 3(m + 2) = m(m — 2)
Find an equation in standard form with integral coefficients that has the
given solution set.
Sample 2
Solution
-4}
- 1)(x + 4) = 0
3(x — 2
Multiply by 3
for integral
coefficients.
+ 4) = 0
(3x — 2)(x + 4) = 0
3x2 + 10x — 8 = 0 Answer
51. 2' —21
49. {2, —3}
52. {
C 55.
—
3'
—
54. { --1 2
1}
2'5
Supply the missing reasons in the proof of: If ab = 0, then a = 0 or b = 0.
Case 1: If a = 0, then the theorem is true; there is nothing to prove.
Case 2: Suppose that a 0 and show that then b = 0.
a. Given
ab = 0
a.
b
b. 1 exists
a
1
1
c.
71 (ab) = —a-(0)
d.
a (ab) = 0
d
a)b = 0
e
1• b = 0
b=0
f.
g
e.
a
f.
g.
?
Mixed Review Exercises
Evaluate if x = 2 and y = 4.
1. (x — y)
4. (5x) 3
7. 4(x + y) 2
2. x4 • y2
5. 4x + y 2
8. (yx)2
3. 5x3
6. 4x2 + y
9. y 2x2
Simplify.
10. (3x3y)(-2xy5)
11. (9a) 3
12.
—
5(x + 2)
Factoring Polynomials
233
5-13 Using Factoring to Solve Problems
Objective
To solve problems by writing and factoring quadratic equations.
The problems in this lesson all lead to polynomial equations that can be solved
by factoring. Sometimes a solution of an equation may not satisfy some of the
conditions of the problem. For example, a negative number cannot represent a
length or an age. You reject solutions of an equation that do not make sense for
the problem.
Example 1 A decorator plans to place a
rug in a 9 m by 12 m room
so that a uniform strip of
flooring around the rug will
remain uncovered. How
wide will this strip be if
the area of the rug is to be
half the area of the room?
Solution
Step 1 The problem asks for the
width of the strip.
Step 2 Let x = the width of the strip.
Then 12 — 2x = the length
of the rug and 9 — 2x = the
width of the rug.
Step 3
9m
Area of the rug = (Area of the room)
(12 — 2x)(9 — 2x) = • 9 • 12
Step 4 108 — 42x + 4x2 = 54
4x2 — 42x + 54 = 0
2(2x2 — 21x + 27) = 0
2[(2x — 3)(x — 9,)] = 0
or
2x — 3 = 0
x= —32 ' or 1.5
2m
x— 9 = 0
x=9
When x = 1.5, the area of the rug When x = 9, the length,
is (12 — 2x)(9 — 2x) = 9 • 6 = 54 12 — 2x, and width, 9 — 2x,
are negative. Since a negative
= —1 (Area of the room) ✓
2length or width is meaningless, reject x = 9 as an answer.
the strip around the rug will be 1.5 m wide. Answer
Step 5 Check:
234
Chapter 5
The equation in Step 3 of Example 1 has a root that does not check because this equation does not meet the "hidden" requirements that the rug have
positive length (12 — 2x > 0) and positive width (9 — 2x > 0). Usually it is
easier to write only the equation and then check its roots against other conditions stated or implied in the problem.
In the next example both solutions of the equation satisfy the conditions of
the problem. You can use the formula
h = rt — 4.9t2
to obtain a good approximation of the height h (in meters) of an object t seconds
after it is projected upward with an initial speed of r meters per second (m/s).
Example 2 An arrow is shot upward with an initial speed of 34.3 m/s. When will it be at
a height of 49 m?
Solution
Step 1 The problem asks for the time when the arrow is 49 m high.
Step 2 Let t = the number of seconds after being shot that the arrow is 49 m high.
Let h = the height of arrow = 49 m. Let r = initial speed = 34.3 m/s.
Step 3 Substitute in the formula:
h = rt — 4.9t2
49 = 34.3t — 4.9t2
4.9t2 — 34.3t + 49 = 0
4.9(t2 — 7t + 10) = 0
4.9(t — 2)(t — 5) = 0
Step 4
Completing the solution and checking the result are left for you.
A calculator may be helpful.
the arrow is 49 m high both 2 s and 5 s after being shot. Answer
Problems
Solve.
A 1. If a number is added to its square, the result is 56. Find the number.
2. If a number is subtracted from its square, the result is 72. Find the number.
3. A positive number is 30 less than its square. Find the number.
4. A negative number is 42 less than its square. Find the number.
5. Find two consecutive negative integers whose product is 90.
6. Find two consecutive positive odd integers whose product is 143.
7. The sum of the squares of two consecutive positive even integers is 340.
Find the integers.
8. The sum of the squares of two consecutive negative even integers is 100.
Find the integers.
Factoring Polynomials
235
Solve.
9. The length of a rectangle is 8 cm greater than its width. Find the dimensions of the rectangle if its area is 105 cm 2 .
10. The length of a rectangle is 6 cm less than twice its width. Find the dimensions of the rectangle if its area is 108 cm 2 .
1. Find the dimensions of a rectangle whose perimeter is 46 m and whose
area is 126 m2 . (Hint: Let the width be w. Use the perimeter to find the
length in terms of w.)
12. Find the dimensions of a rectangle whose perimeter is 42 m and whose
area is 104 m2 .
13. The sum of two numbers is 25 and the sum of their squares is 313. Find
the numbers. (Hint: Let one of the numbers be x. Express the other number
in terms of x.)
0
The difference of two positive numbers is 5 and the sum of their squares is
233. What are the numbers?
15. Originally the dimensions of a rectangle were 20 cm by 23 cm. When both
dimensions were decreased by the same amount, the area of the rectangle
decreased by 120 cm 2 . Find the dimensions of the new rectangle.
16. Originally a rectangle was twice as long as it was wide. When 4 m were
added to its length and 3 m subtracted from its width, the resulting rectangle had an area of 600 m 2 . Find the dimensions of the new rectangle.
In Exercises 17-23, use the formula h = rt — 4.9t2 where h is in meters and
the formula h = rt — 1612 where h is in feet. A calculator may be helpful.
B
A ball is thrown upward with an initial speed of 24.5 m/s. When is it
19.6 m high? (Two answers)
18. A rocket is fired upward with an initial speed of 1960 m/s. After how
many minutes does it hit the ground?
lJ A batter hit a baseball upward with
an initial speed of 120 ft/s. How
much later did the catcher catch it?
20. Mitch tossed an apple to Kathy, who
was on a balcony 40 ft above him,
with an initial speed of 56 ft/s. Kathy
missed the apple on its way up, but
caught it on its way down. How long
was the apple in the air?
21. A signal flare is fired upward with
initial speed 245 m/s. A stationary
balloonist at a height of 1960 m sees
the flare pass on the way up. How
long after this will the flare pass the
balloonist again on the way down?
236
Chapter 5
22. A ball is thrown upward from the top of a 98 m tower with initial speed
39.2 m/s. How much later will it hit the ground? (Hint: Consider the top of
the tower as level zero. If h is the height of the ball above the top of the
tower, then h = —98 when the ball hits the ground.)
23. A rocket is fired upward with an initial velocity of 160 ft/s.
a. When is the rocket 400 ft high?
b. How do you know that 400 ft is the greatest height the rocket reaches?
Solve.
24. A garden plot 4 m by 12 m has one
side along a fence as shown at the
right. The area of the garden is to be
doubled by digging a border of uniform
width on the other three sides. What
should the width of the border be?
fence
4 in
garden
12 m
fence
25. Vanessa built a rectangular pen for her
dogs. She used an outside wall of the
garage for one of the sides of the pen.
She had to buy 20 m of fencing in
order to build the other sides of the
pen. Find the dimensions of the pen
if its area is 48 m2 .
26. A rectangular garden 30 m by 40 m
has two paths of equal width crossing
through it as shown. Find the width
of each path if the total area covered
by the paths is 325 m2 .
30 m
27. A box has a square bottom and top
40m
and is 5 cm high. Find its volume
if its total surface area is 192 cm 2 .
28. The bottom and top of a box are rectangles twice as long as they are wide.
Find the volume of the box if it is 4 ft high and has a total surface area of_
220 ft2 .
29. A 50 m by 120 m park consists of a rectangular lawn surrounded by a path
of uniform width. Find the dimensions of the lawn if its area is the same as
the area of the path. (Hint: Let x = the width of path.)
C 30. The Parkhursts used 160 yd of fencing to enclose a rectangular corral and
to divide it into two parts by a fence parallel to one of the shorter sides.
Find the dimensions of the corral if its area is 1000 yd 2 .
31. Each edge of one cube is 2 cm longer than each edge of another cube. The
volumes of the cubes differ by 98 cm 3 . Find the lengths of the edges of
each cube.
Factoring Polynomials
237
32. A rectangular sheet of metal is 10 cm
longer than it is wide. Squares, 5 cm on a
side, are cut from the corners of the sheet,
and the flaps are bent up to form an opentopped box having volume 6 L. Find the
original dimensions of the sheet of metal.
You may wish to make a model.
(Recall that 1 L = 1000 cm3 .)
Mixed Review Exercises
Simplify.
1. (8a2b)(2ab2)
2. (5a2)3
3. 3a(4 — 2b)
4. (6r) (3
5. (8)(16n — 24p)
6. (-28x — 14y)(-4)
7. (3a + 2)(2a2 + 5 — 7a)
8. (3b2y) 2
9. 6x(x2 — 8)
Factor completely.
10. —28 + 6m + 10m2
13. y4 — y 3 — 12y2
11. 36a3 — 9ab2
14. 15m2 + 26mn + 8n2
21n2 + 22n — 8
5. 3 + 10x2 — 17x
Self-Test 4
Vocabulary factor completely (p. 227)
converse (p. 230)
polynomial equation (p. 231)
linear equation (p. 231)
quadratic equation (p. 231)
cubic equation (p. 231)
standard form of a polynomial equation (p. 231)
Factor completely.
1. 7r — 3rt + 7s — 3st
3. 18a3 — 12a2 + 2a
n2 — 2n + 1 — 100e
4. 21xy — 18x2 — 6y2
Obj. 5-10, p. 224
Obj. 5-11, p. 227
Solve.
5.
-
4k = 32
6. 5m2 + 20m + 20 = 0
8. z3 = z2 + 30z
7. a3 = 169a
9. The length of a rectangle is 9 cm more than its width.
The area of the rectangle is 90 cm 2 . Find the dimensions
of the rectangle.
Check your answers with those at the back of the book.
238
Chapter 5
Obj. 5-12, p. 230
Obj. 5-13, p. 234
© Copyright 2025