PROBLEM 16.4
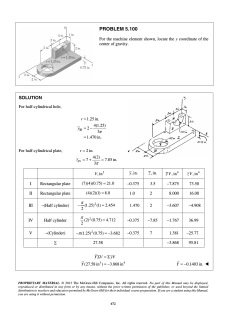
PROBLEM 16.4 The motion of the 2.5-kg rod AB is guided by two small wheels which roll freely in horizontal slots. If a force P of magnitude 8 N is applied at B, determine (a) the acceleration of the rod, (b) the reactions at A and B. SOLUTION ΣFx = Σ( Fx )eff : P = ma (a) a= P 8N = = 3.20 m/s 2 m 2.5 kg a = 3.20 m/s 2 2r 2r ΣM B = Σ( M B )eff : W r − − Ar = ma π π (b) 2 2 2 2 A = W 1 − − ma = mg 1 − − P π π π π 2 2 = (2.5 kg)(9.81 m/s 2 ) 1 − − (8 N) π π = 8.912 N − 5.093 N = 3.819 N A = 3.82 N ΣFy = 0: A + B − W = 0 B = W − A = (2.5)(9.81) − 3.819, B = 20.71 N PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1407 PROBLEM 16.19 The triangular weldment ABC is guided by two pins that slide freely in parallel curved slots of radius 6 in. cut in a vertical plate. The weldment weighs 16 lb and its mass center is located at Point G. Knowing that at the instant shown the velocity of each pin is 30 in./s downward along the slots, determine (a) the acceleration of the weldment, (b) the reactions at A and B. SOLUTION v = 30 in./s Slot: an = v 2 (30 in./s)2 = = 150 in./s 2 r 6 in. a n = 12.5 ft/s 2 at = at Weldment is in translation 30° 60° an = 12.5 ft/s 2 60° ΣF = ΣFeff : mg cos 30° = mat at = 27.886 ft/s 2 (a) 60° Acceleration β = tan −1 an 12.5 = tan −1 = 24.14° 27.886 at a 2 = at2 + an2 = (27.886) 2 + (12.5) 2 a = 30.56 ft/s 2 84.1° a = 30.6 ft/s 2 84.1° PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1428 PROBLEM 16.19 (Continued) (b) Reactions ma = 16 lb (30.56 ft/s 2 ) = 15.185 lb 2 32.2 ft/s ΣM A = Σ( M A )eff : B cos 30°(9 in.) − (16 lb)(6 in.) = (15.185 lb)(cos84.14°)(3 in.) − (15.185 lb)(sin 84.14°)(6 in.) 7.794 B − 96 = + 4.651 − 90.634 B = +1.285 lb B = 1.285 lb 30° ΣFx = Σ( Fx )eff : A cos 30° + B cos 30° = ma cos84.14° A cos 30° + (1.285 lb) cos 30° = (15.185 lb) cos84.14° A cos 30° + 1.113 lb = 1.550 lb A = +0.505 lb A = 0.505 lb 30° PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1429 PROBLEM 16.25 The rotor of an electric motor has an angular velocity of 3600 rpm when the load and power are cut off. The 50-kg rotor, which has a centroidal radius of gyration of 180 mm, then coasts to rest. Knowing that kinetic friction results in a couple of magnitude 3.5 N ⋅ m exerted on the rotor, determine the number of revolutions that the rotor executes before coming to rest. SOLUTION I = mk 2 = (50)(0.180) 2 = 1.62 kg ⋅ m 2 M = I α: 3.5 N ⋅ m = (1.62 kg ⋅ m 2 )α α = 2.1605 rad/s 2 (deceleration) 2π 60 = 120π rad/s ω0 = 3600 rpm ω 2 = ω02 + 2αθ 0 = (120π rad/s) 2 + 2(−2.1605 rad/s 2 )θ θ = 32.891 × 103 rad = 5235.26 rev θ = 5230 rev or PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1439 PROBLEM 16.48 A uniform slender rod AB rests on a frictionless horizontal surface, and a force P of magnitude 0.25 lb is applied at A in a direction perpendicular to the rod. Knowing that the rod weighs 1.75 lb, determine (a) the acceleration of Point A, (b) the acceleration of Point B, (c) the location of the point on the bar that has zero acceleration. SOLUTION W g 1 W 2 I= L 12 g m= ΣFx = Σ( Fx )eff : P = ma = a= ΣM G = Σ( M G )eff : P W a g P 0.25 lb 1 g= g= g W 1.75 lb 7 a= 1 g 7 L 1 W 2 Lα = Iα = 2 12 g α =6 P 5 0.25 lb g 6 g =6 ⋅ = W L 1.75 lb L 7 L α= 6g 7L We calculate the accelerations immediately after the force is applied. After the rod acquires angular velocity, there will be additional normal accelerations. (a) Acceleration of Point A. aA = a + (b) L 1 L 6 4 4 α = g + ⋅ g = g = (32.2 ft/s2 ) 2 7 2 7 7 7 a A = 18.40 ft/s 2 a B = 9.20 ft/s 2 Acceleration of Point B. aB = a − L 1 L 6 2 2 α = g − ⋅ g = − g = − (32.2 ft/s2 ) 2 7 2 7 7 7 PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1478 PROBLEM 16.48 (Continued) (c) Point of zero acceleration. aP = 0 a − ( z P − zG )α = 0 z P − zG = Since zG = a α = 1 g 7 6 g ⋅ 7 L = 1 L 6 1 L 2 1 1 2 L+ L= L 2 6 3 2 z P = (36 in.) 3 zP = z P = 24.0 in. PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1479 PROBLEM 16.56 The 80-g yo-yo shown has a centroidal radius of gyration of 30 mm. The radius of the inner drum on which a string is wound is 6 mm. Knowing that at the instant shown the acceleration of the center of the yo-yo is 1 m/s2 upward, determine (a) the required tension T in the string, (b) the corresponding angular acceleration of the yo-yo. SOLUTION W = mg W = 0.080 kg (9.81 m/s 2 ) = 0.7848 N ΣFy = Σ( Fy )eff : T − W = W a g T − (0.08 kg)(9.81 m/s 2 ) = (0.08 kg)(1 m/s 2 ) T = 0.8648 N (a) T = 0.865 N Tension in the string. ΣM G = Σ( M G )eff : Tr = Iα (0.8648 N)(0.006 m) = mk 2α 5.1888 × 10−3 N ⋅ m = (0.08 kg)(0.03 m)2 α (b) Angular acceleration. α = 72.067 rad/s 2 α = 72.1 rad/s 2 PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1488 PROBLEM 16.64 A beam AB of mass m and of uniform cross section is suspended from two springs as shown. If spring 2 breaks, determine at that instant (a) the angular acceleration of the beam, (b) the acceleration of Point A, (c) the acceleration of Point B. SOLUTION ΣFy = 2mg = maG 3 1 mg L mL2α ΣM G = = 3 2 12 aG = (a) (b) aA = 2g 2 g L + 3 L 2 = 2g 3 , α = 2g L g 3 , g 3 5g 3 aA = (c) aB = 2g 2 g L + 3 L 2 = 5g 3 aB = PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1499 PROBLEM 16.76 A uniform slender rod of length L = 900 mm and mass m = 4 kg is suspended from a hinge at C. A horizontal force P of magnitude 75 N is applied at end B. Knowing that r = 225 mm, determine (a) the angular acceleration of the rod, (b) the components of the reaction at C. SOLUTION (a) Angular acceleration. a = rα I = 1 mL2 12 L ΣM C = Σ( M C )eff : P r + = (ma )r + Iα 2 1 mL2α 12 L 2 1 2 P r + = m r + L α 2 12 = (mrα )r + Substitute data: 0.9 m 1 = (4 kg) (0.225 m) 2 + (0.9 m)2 α (75 N) 0.225 m + 2 12 50.625 = 0.4725α α = 107.14 rad/s 2 (b) α = 107.1 rad/s 2 Components of reaction at C. ΣFy = Σ( Fy )eff : C y − W = 0 C y = W = mg = (4 kg)(9.81 m/s 2 ) C y = 39.2 N ΣFx = Σ( Fx )eff : C x − P = −ma Cx = P − ma = P − m(r α ) = 75 N − (4 kg)(0.225 m)(107.14 rad/s 2 ) Cx = 75 N − 96.4 N = −21.4 N C x = 21.4 N PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1527 PROBLEM 16.86 A 12-lb uniform plate rotates about A in a vertical plane under the combined effect of gravity and of the vertical force P. Knowing that at the instant shown the plate has an angular velocity of 20 rad/s and an angular acceleration of 30 rad/s2 both counterclockwise, determine (a) the force P, (b) the components of the reaction at A. SOLUTION 6 at = rα = ft (30 rad/s 2 ) = 15 ft/s 2 12 6 an = rω 2 = ft (20 rad/s) 2 = 200 ft/s 2 12 Kinematics. Mass and moment of inertia. I= m= W 12 lb = = 0.37267 lb ⋅ s 2 /ft g 32.2 ft/s 2 2 2 m 10 20 + = (0.37267 lb ⋅ s 2 /ft)(0.28935 ft 2 ) = 0.10783 lb ⋅ s 2 ⋅ ft 12 12 12 Kinetics. (a) Force P. 16 6 6 ΣM A = Σ( M A )eff : P ft − W ft = mat ft + I α 12 12 12 4 1 1 P = (12) + (0.37267)(15) + (0.10783)(30) 3 2 2 P = 9.0224 lb. P = 9.02 lb PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1537 PROBLEM 16.86 (Continued) (b) Reaction at A. ΣFy = Σ( Fx )eff : Ax = − man = − 12 (200) 32.2 Ax = −74.53 lb A x = 74.5 lb ΣFy = Σ( Fy )eff : Ay + P − W = mat Ay = W + mat − P = 12 + 12 (15) − 9.02 = 8.57 lb 32.2 A y = 8.57 lb PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1538 PROBLEM 16.98 A drum of 60-mm radius is attached to a disk of 120-mm radius. The disk and drum have a total mass of 6 kg and a combined radius of gyration of 90 mm. A cord is attached as shown and pulled with a force P of magnitude 20 N. Knowing that the disk rolls without sliding, determine (a) the angular acceleration of the disk and the acceleration of G, (b) the minimum value of the coefficient of static friction compatible with this motion. SOLUTION a = rα = (0.12 m)α I = mk 2 = (6 kg)(0.09 m) 2 I = 48.6 × 10−3 kg ⋅ m 2 ΣM C = Σ( M C )eff : (20 N)(0.12 m) = (ma ) r + I α 2.4 N ⋅ m = (6 kg)(0.12 m) 2 α + 48.6 × 10−3 kg ⋅ m 2 2.4 = 135.0 × 10−3 α α = 17.778 rad/s 2 (a) α = 17.78 rad/s 2 a = 2.13 m/s 2 a = rα = (0.12 m)(17.778 rad/s 2 ) = 2.133 m/s 2 (b) ΣFy = Σ( Fy )eff : N − mg = 0 N = (6 kg)(9.81 m/s 2 ) N = 58.86 N ΣFx = Σ( Fx )eff : 20 N − F = ma 20 N − F = (6 kg)(2.133 m/s 2 ) F = 7.20 N ( μ s ) min = F 7.20 N = N 58.86 N ( μ s ) min = 0.122 PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1558 PROBLEM 16.117 The ends of the 20-lb uniform rod AB are attached to collars of negligible mass that slide without friction along fixed rods. If the rod is released from rest when θ = 25°, determine immediately after release (a) the angular acceleration of the rod, (b) the reaction at A, (c) the reaction at B. SOLUTION Kinematics: Assume α ω=0 ] + [4α a B = a A + a B/A = [ a A 25°] aB = (4α ) cos 25° = 3.6252α a A = (4α )sin 25° = 1.6905α ] + [2α aG = a A + aG/ A = [ a A aG = [1.6905α ] + [2α ax = (aG ) x = [1.6905α 25°] 25°] ] + [0.84524α ] ax = 0.84524α a y = [2α cos 25° ] = 1.8126α We have found for α ax = 0.84524α a y = 1.8126α Kinetics: I = 1 1 mL2 = m(4 ft) 2 12 12 PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1588 PROBLEM 16.117 (Continued) (a) Angular acceleration. ΣM E = Σ( M E )eff : mg (1.8126 ft) = I α + max (0.84524 ft) + ma y (1.8126 ft) mg (1.8126) = 1 m(4) 2 α + m(0.84524)2 α + m(1.8126) 2α 12 g (1.8126) = 5.3333α (b) α = 0.33988g ΣFy = Σ( Fy )eff : A − mg = −ma y = m(1.8126α ) 20 A − 20 = − (1.8126)(10.944) 32.2 A = 20 − 12.321 = 7.6791 lb (c) α = 10.944 rad/s 2 ΣFx = Σ( Fx )eff : A = 7.68 lb B = max = m(0.84524α ) 20 (0.84524)(10.944) 32.2 B = 5.7453 lb B= B = 5.75 lb PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1589 PROBLEM 16.125 The 7-lb uniform rod AB is connected to crank BD and to a collar of negligible weight, which can slide freely along rod EF. Knowing that in the position shown crank BD rotates with an angular velocity of 15 rad/s and an angular acceleration of 60 rad/s2, both clockwise, determine the reaction at A. SOLUTION Crank BD: 4 ω BD = 15 rad/s, v B = ft (15 rad/s) = 5 ft/s 12 α BD = 60 rad/s 2 4 (a B ) x = ft (60 rad/s 2 ) = 20 ft/s 2 12 4 (a B ) y = ft (15 rad/s) 2 = 75 ft/s 2 12 Rod AB: Velocity: Instantaneous center at C. 25 CB = ft / tan 30° = 3.6084 ft 12 ω AB = vB 5 ft/s = = 1.3856 rad/s CB 3.6084 ft Acceleration: (a A/B )t = ( AB )α AB = 25 α AB 12 25 2 (a A /B ) n = ( AB)ω AB = (1.3856)2 = 4 ft/s 2 12 (aG/B )t = (GB)α AB = 12.5 α AB 12 PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1602 PROBLEM 16.125 (Continued) (aG /B ) n 12.5 2 2 2 = (GB)ω AB = (1.3856) = 2 ft/s 12 a A = a B + a B/A = a B + (a B/A )t + (aG/A ) n [a A 30°] = [20 a A cos 30° = 20 − 4; (18.475) sin 30° = 75 − 25 ] + [75 ] + α AB 12 a A = 18.475 ft/s 2 + [4 ] 30° 25 α AB ; α AB = 31.566 rad/s 2 12 a = a B + aG/B = a B + (aG/B )t + (aG/B )n a = [20 ] + [75 ] + [ 12.5 (31.566) ] + [2 12 ax = 20 − 2 = 18; ] ax = 18 ft/s 2 a y = 75 − 32.881 = 42.119; a y = 42.119 ft/s 2 2 Kinetics: I = 1 7 lb 25 m( AB )2 = ft = 0.078628 slug ⋅ ft 2 12 12(32.2) 12 25 12.5 12.5 ft − mg ft = − I α AB + ma y ft ΣM B = Σ( M B )eff : ( A sin 60°) 12 12 12 12.5 7 12.5 1.8042 A − (7 lb) ft = −(0.078628 slug ⋅ ft 2 )(31.566 rad/s 2 ) + slug (42.119 ft/s 2 ) ft 12 32.2 12 1.8042 A − 7.2917 = −2.4820 + 9.5378 A = 7.9522 lb A = 7.95 lb 60° PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1603 PROBLEM 16.134 Two 8-lb uniform bars are connected to form the linkage shown. Neglecting the effect of friction, determine the reaction at D immediately after the linkage is released from rest in the position shown. SOLUTION Kinematics: Bar AC: Rotation about C 15 a = ( BC )α = ft α 12 a = 1.25α sin θ = 15 in. θ = 30° 30 in. Bar BC: a D/B = Lα Must be zero since aD α BD = 0 and aBD = a Kinetics: Bar BD ΣFy = Σ( Fy )eff : By − W = − ma 8 lb (1.25α ) 32.2 By = 8 − 0.3105α By − 8 lb = − (1) PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1621 PROBLEM 16.134 (Continued) ΣM B = Σ( M B )eff : D (2.165 ft) − W (0.625 ft) = − ma (0.625 ft) 8 lb (1.25α )(0.625 ft) 32.2 D = 2.309 − 0.08965α D (2.165 ft) − (8 lb)(0.625 ft) = − (2) 1 m( AC ) 2 12 1 8 lb = (2.5 ft) 2 12 32.2 = 0.1294 lb ⋅ ft ⋅ s 2 I = Bar AC: ΣM C = Σ( M C )eff : W (1.25 ft) + By (1.25 ft) = I α + m(1.25α )(1.25) Substitute from Eq. (1) for By 8 (1.25) 2 α 32.2 10 + 10 − 0.3881α = 0.1294α + 0.3882α 20 = 0.9057α 8(1.25) + (8 − 0.3105α )(1.25) = (0.1294)α + α = 22.08 rad/s 2 Eq. (2), D = 2.309 − 0.08965α = 2.309 − 0.08965(22.08) = 2.309 − 1.979 D = 0.330 lb D = 0.330 lb PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed, reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual, you are using it without permission. 1622
© Copyright 2025