1. real estate
2. buying and selling homes

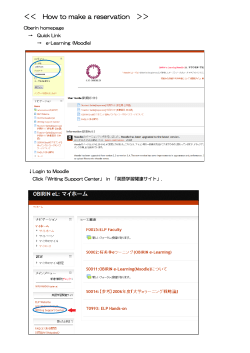
Controlling for Variable Liquidity and Selection Bias
in Indices of Private Asset Market Values
by
∗
Jeffrey Fisher
Indiana University
∗
Dean Gatzlaff
The Florida State University
∗
David Geltner
University of Cincinnati
∗
Donald Haurin
The Ohio State University
Working Paper:
Comments welcome.
This version March 13, 2002
The authors thank the Real Estate Research Institute (RERI) for financial support of this study. We also
thank Jim Clayton and participants at the 2002 American Real Estate &Urban Economics Association
Annual Meeting for helpful comments on an earlier version of this paper under a different title.
Indiana University; School of Business; Center for Real Estate Studies; Bloomington, IN 47405; phone: 812.855.7794; fax:
812.855.8679; email: fisher@indiana.edu
∗
The Florida State University; College of Business; Tallahassee, FL 32306-1110;
phone: 850.644.5710; fax: 850.644.4077; email: dgatzla@garnet.acns.fsu.edu
∗∗
University of Cincinnati; College of Business Administration; P.O. Box 210195; Cincinnati, OH 45221-0195; phone:
513.556.7071; fax: 513.556.4891; email: david.geltner@uc.edu
∗∗∗
The Ohio State University; Departments of Economics and Finance; 1945 N. High Street; Columbus, OH 43210; phone:
614.292.0482; fax: 614.292.9530; email: haurin.2@osu.edu
Controlling for Variable Liquidity and Selection Bias
in Indices of Private Asset Market Values
Fisher, Gatzlaff, Geltner, and Haurin
Abstract
This paper develops the concept of a constant-liquidity value index for private asset markets
and an econometric procedure for estimating such an index. We demonstrate this procedure on the
NCREIF database of institutional commercial property. Private asset markets are distinguished from
public securities exchanges in that unique, whole assets are individually traded in privately negotiated
deals between one selling party and one buying party, and there is no institutional structure set up to
maintain liquidity in the sense of ease of selling of the assets. Major private asset markets in the U.S.
include commercial and residential real estate, collectibles, and private equity markets such as the
venture capital market. Liquidity in such markets, as indicated by the volume (or rate) of asset sale
transactions, or the rate of capital flow into the market, is notoriously variable over time. Indeed, a
salient characteristic of private asset markets is that liquidity is high when the market is “up”, and low
when the market is “down”. Therefore, indices of changes in market value over time that are based on
asset transaction prices will systematically reflect variable liquidity. This renders “apples-to-apples”
comparisons problematical; both in the comparison of asset values across time within the market (i.e.,
measurement of “capital returns”), and in the comparison of investment return volatility between the
private asset market and other markets or asset classes, especially publicly-traded securitized
investment asset classes where liquidity is constantly maintained by the stock exchange.
In this paper we present a model of dynamic equilibrium in a double-sided search market
with a finite supply of heterogeneous assets and agents, the major characteristics of private asset
markets. We show how such a model represents the type of pro-cyclical variable liquidity observed in
private asset markets, and we define a conceptual construct which we call “constant liquidity value”,
to reflect the prices that would hypothetically equilibrate such a market holding the ease of selling
constant across time within the market. We show the theoretical implications this model holds for the
relationship between variable liquidity price changes and constant liquidity value changes across time
in such a market. Depending on whether the liquidity cycle is coincident with the asset market cycle
in levels or in changes, constant-liquidity values will either display greater cycle amplitude or a
temporal lead compared to the variable liquidity prices. We then develop an econometric model that
allows empirical quantification of the difference between observed price changes and constantliquidity value changes for a population of assets with known characteristics of both the sold and
unsold assets in each period. We also explore the effect of sample selection bias in transaction-based
indices, and we correct for this type of bias in our suggested empirical procedure. Our application to
the NCREIF database reveals that, in the case of institutional commercial real estate investment,
constant liquidity values tend to lead variable-liquidity prices in time, and also to display greater
volatility and cycle amplitude.
I. Introduction
Measuring and monitoring changes in investment values is fundamental to understanding any
investment asset class, including those traded in private markets, such as real estate, collectibles, and
venture capital. This problem has received particular attention in the private real estate investment
industry, where there has long been a recognized need to compare real estate risk and return to that of
other asset classes, such as publicly-traded bonds and stocks (including REITs). The housing industry and
policy makers have also long been interested in tracking home values meaningfully over time. Recently,
2
there has been increasing interest in tracking private equity investment returns, such as the performance
of the venture capital investment industry. Yet such measurement of private asset market price changes or
capital returns faces serious problems, both conceptual and empirical.
The most basic problem is the difficulty of measuring market value movements in an
environment where whole, heterogeneous assets are traded infrequently and irregularly over time,
typically between a single selling party and a single buying party. Individual asset sale prices provide
asynchronous, idiosyncratic, and noisy indications of market value. Another potential problem is posed by
the fact that typically only a fraction of all the assets in the market population transact during any given
period, and those that transact are not a random sample of the population. This causes sample selection
bias in empirical analysis. A third fundamental problem is posed by the phenomenon that private asset
markets typically display highly variable liquidity over time. During “up” markets, capital flows into the
sector, there is much greater volume of trading, and it is much easier to sell assets. Just the opposite
typically occurs in “down” markets. This renders empirically observable prices “apples versus oranges”
for comparisons across time or between private asset markets and the constantly liquid public securities
markets.
The first two of these problems have been addressed extensively in the economics of search, real
estate economics, and statistics literature, and to some extent more recently in the financial economics
literature. Econometric procedures for estimating transaction price-based indices of periodic market value
changes have been developed and honed over the past several decades, including the hedonic value model
developed by Rosen (1974) and the related constant quality price index procedure of Court (1939) and
Griliches (1961), and the repeat-sales regression pioneered by Bailey, Muth & Nourse (1963). These
procedures allow the estimation of a periodic market value change index from noisy, asynchronous,
heterogeneous asset prices.1 The problem of identifying and correcting sample selection bias has been
1
Subsequent further developments in these procedures in the real estate economics literature have included, among
others, Bryan & Colwell (1982), Case & Shiller (1987), Shiller (1991), Clapp & Giacotto (1992), and Goetzmann
(1992). A related approach is the use of “appraised values” or “assessed valuations” derived from asset valuation
professionals. Asset market value indices are now produced from regularly conducted professional valuations in the
real estate and venture capital industries (e.g., the NCREIF Index in real estate, the Venture One or Venture
Economics series in the venture capital industry). Recently, regression-based valuation models of venture capital
3
addressed in general by Heckman (1976, 1979), and more recently applied specifically to real estate
markets in several studies, including Gatzlaff & Haurin (1997, 1998).2 While the present paper will
include these solutions, our primary focus is on the third problem of private asset market price indices
noted above, that of variable liquidity in the observable transaction price data. Although the phenomenon
of pro-cyclical variable liquidity in private asset markets has been widely noted in the practitioner and
trade literature, the only previous attempts that we know of in the academic literature to quantitatively
control for this problem in the construction of market value indices have been so-called “de-lagging,” or
reverse filter, procedures that have been applied to appraisal-based indices of commercial property
values.3 We address the variable liquidity problem by developing the concept of a “constant liquidity
value” index for private asset markets.
The remainder of this paper is organized as follows. Section II presents a theoretical model of the
difference between empirically observable (variable-liquidity) prices and hypothetical values that would
reflect constant liquidity over time (that is, prices that would hold constant the ease of selling), in a
private asset market. Section III develops an econometric model that allows empirical quantification of
the difference between observed prices and constant-liquidity values for a population of assets with
known characteristics of both the sold and unsold assets in each period. This model also provides for the
correction of sample selection bias, adapting the classical Heckman procedure to the double-sided search
market context that well represents private asset markets. Sections IV and V describe the data and
empirical results, respectively, for our application of the model developed here to the NCREIF database
of commercial real estate, producing a constant liquidity value index of real estate capital returns. Section
VI concludes the paper.
firms similar in form to the real estate hedonic value models, only based on professional valuations of venture
capital firms, have been used in the financial economics literature (e.g., Gompers & Lerner (2000)).
2
The Gompers & Lerner (2000) study of the venture capital market also employed the Heckman correction
procedure.
3
See, for example, Fisher, Geltner & Webb (1994), and Fisher & Geltner (2000). However, these procedures do not
explicitly or separately identify and control for the effect of variable liquidity on market value changes.
4
II. A Model of Variable Liquidity in a Double-Sided Search Market with a Finite Supply of
Heterogeneous Assets and Agents
Define liquidity in a private asset market as the rate of asset transaction volume (reflecting the
density of the market or the rate of capital inflow into the sector), and consider two stylized empirical facts
about liquidity that are widely believed by practitioners to apply to most of the major private asset markets in
the U.S:
•
Liquidity tends to vary across time. When the market is more liquid, asset owners can sell more
assets, or sell any given asset quicker and easier (holding price constant). Alternatively (and
equivalently), greater liquidity implies that asset owners can sell the same number of assets (or any
given asset in the same amount of time) at higher prices (other things being equal).
•
Liquidity is positively correlated with the asset market cycle. That is, liquidity is typically greater
when the market is up (asset prices are relatively high and/or are rising), and vice versa, liquidity is
less when the market is down (prices relatively low or falling).
Next consider the implications that this type of pro-cyclical variable liquidity holds for attempts
to empirically measure historical value movements in the private asset market, and to compare the capital
risk and return characteristics of that market (or investment asset class) to that of public exchange-traded
securities. Empirically observable asset transaction prices reflect the pro-cyclical variation in liquidity
described above. Therefore, indices based on transaction prices will systematically reflect variable
liquidity, rendering apples-to-apples comparisons problematic, both in the comparison of the private asset
market values across time (i.e., in the computation of capital returns across different phases of the asset
market cycle), and in the comparison of capital return volatility between the private asset market and
public exchange-traded securitized investment asset classes such as stocks and bonds. The price level
indicated by the private market index during periods of peak liquidity will reflect greater ease of selling
than the price level indicated by the index during periods of low liquidity. Periodic capital returns derived
from the index, and the historical volatility indicated by those returns, will reflect variation across time in
the ability to actually realize the implied returns. This is in contrast to indices of publicly-traded
5
securities’ returns, which reflect asset prices that are effectively always liquid for practical purposes in the
sense defined here, at least for most investors.4
Another perspective on the implications of variable liquidity for price index construction can be
seen in the relationship between the definition of “market value” and the classical economic concept of
opportunity cost (or opportunity value). The concept of market value in private asset markets traditionally
involves at best a vague and ambiguous reference to variation in liquidity. For example, in the real estate
appraisal profession, market value is defined simply as the expected transaction price as of a given point
in time, assuming reasonable exposure to the market. Market value is thus the probabilistic mean of the
distribution of potential transaction prices for the subject asset as of the current time. But, is this value,
estimated (in principle) from the mean of a contemporaneous transaction price distribution (of the sale of
similar assets, adjusted for quality differences), appropriate no matter how few are the transactions or
how long it might take or how difficult it might be to sell a similar asset in the current market?
Such a definition of value is problematic from an economic opportunity cost perspective, as well
as from the practical perspective of allowing apples-to-apples comparisons with stock market returns. The
variable-liquidity conception of market value defined in traditional practice would allow for asset
valuation more akin to a limit order price in the stock market, in which a broker is requested to buy (or
sell) a stock at the specified price if possible. In the stock market no one confuses limit order prices for
market prices. In contrast, a value definition more useful for private asset market investment analysis
would conform to the economic concept of opportunity cost (or value). This concept embodies a
constraint on how long it will take (or how difficult it will be) to sell (or buy) at the value in question.
4
Liquidity is defined and measured in various ways in the financial economics literature studying public securities
markets. Some of these definitions or measures differ from the volume of transaction measure we are employing
here. The concept that underlies the notion of liquidity in the present paper is ease of selling, without discounting the
price below current market value. This concept has a somewhat different practical meaning in private markets
characterized by significant search and transaction costs than it does in public securities markets that are designed to
preserve at all times precisely this definition of liquidity. Thus, at least by the standards familiar to private asset
market investors, it is effectively as easy to sell a publicly-traded stock (at current market value) during a downmarket as during an up-market. (Note that market value is in this case a value established by the operation of the
exchange so as to preserve liquidity while obtaining as high a price as possible for the sellers.) This is not the case in
typical private asset markets, where no such public exchange mechanism exists.
6
From this perspective, it is useful to define a constant liquidity concept of value in which the length of
time or degree of difficulty in selling (or buying) assets is held constant.5
To explore the problem this poses for the construction of an asset transaction price-based index of
private market value, we need a model of the functioning of such a market that can represent the
relationship between observed prices, transaction volume, and constant-liquidity value. The model we
present in this section is a double-sided (buyer and seller) search market model of equilibrium, in which
there is a finite (but large) supply of heterogeneous (but similar) assets and agents (potential buyers and
sellers). Our model is similar in spirit and some of its key technical characteristics to that of Wheaton’s
(1990) model of the housing market. The important implications of this model can be seen with the help
of a series of diagrams of the frequency distributions of potential buyers and sellers in the asset market
over time.
We begin with Figure 1, which depicts the number of potential buyers and sellers (measured on
the vertical axis) during a given period of time. The horizontal axis measures reservation prices for an
asset of a given quality and quantity. The reservation prices are the prices at which potential buyers and
sellers will stop negotiating or searching for a better deal and consummate a transaction. The left-hand
distribution consists of potential buyers, and the right-hand distribution is that of potential sellers (current
owners of the assets). It makes sense for the buyer distribution to be centered to the left of the seller
distribution, because it is to be expected that parties already owning assets (potential sellers) would
generally have higher inherent values for those assets than parties who do not currently own such assets.6
Property characteristics in the population of properties differ, but through a technique such as
hedonic price analysis, they can be compared in a constant-quality framework. In other words,
5
Humorist P.J. O’Rouke expresses the difference between market value and limit order price or opinion of value as
follows: “A thing is worth what people will give for it and it isn’t worth anything else… Smart as you are and dumb
as everybody else is, the market says your shares didn’t sell. And the market is right.” (From P.J. O’Rourke, Eat the
Rich, Atlantic Monthly Press, New York, 1998, page 109.)
6
Note also that the seller distribution represents, essentially, the entire physical stock of the (type of) asset in
question. (Sellers who are effectively “not in the market” can be characterized as having very high reservation
prices.) A salient empirical fact is that not all assets sell every period, which implies that not all of the seller
reservation price distribution consummates transactions. Assuming that the portion of the sellers who do transact
tend to have lower reservation prices than those who do not, the implication is that the buyer reservation price
distribution must be centered to the left of (lower than) the seller reservation price distribution.
7
conceptually we can imagine that the assets themselves are homogeneous (or that we can adjust for crosssectional differences in the assets), and yet there would still be dispersion in the reservation prices across
the owners and potential owners (buyers) of the assets. This dispersion is due to heterogeneity within the
agent populations of the individual potential buyers and sellers. This heterogeneity may reflect different
abilities to profit from the asset (different “inherent value” perceptions), or different knowledge and/or
perception about the nature of the asset or the market, or different search costs and value of time. The
heterogeneity and dispersion represented in Figure 1 does not imply any sort of irrational behavior on the
part of agents, though nothing in this model prevents it from also reflecting irrational or “behavioral”
phenomena if such are present.
----------------------Insert Figure 1
----------------------Now consider what governs the occurrence of transactions. Broadly speaking, transaction
motivations may be considered as coming from either the macro or micro levels. The macro level refers to
broad portfolio-level policy considerations, and may reflect market-wide movements and capital flows.
For example, a class or group of investors may decide to allocate a larger percentage of their overall
portfolio to investment in the subject private asset market. This would trigger a macro-level decision to
buy such assets, and investment managers would find themselves under pressure to buy such assets that
they might otherwise pass by. Effectively, the macro pressure in this case results in an upward adjustment
in the reservation prices of the effected potential buyers. Macro-level transaction motivations may explain
much of the variation over time in the flow of financial capital into and out of asset market segments.
There may be pressure either on the buy side or the sell side, and this may move the buyer or seller
reservation price distributions depicted in Figure 1 along the horizontal axis, including relative movement
either toward, or away, from one another. Such movements underlie changes in market value as well as
changes in liquidity over time. Equilibrium in the market simultaneously determines both price and
volume of trade (per period of time). Note that this model is characterized by a downward-sloping
demand function and upward-sloping supply function in the private asset market. While there may be
8
many similar assets and many similar potential buyers, the supply of neither is infinite. Thus, neither
buyers nor sellers are pure price-takers.7
While broad market movements may be determined by macro-level policy decisions or
widespread market participant behavior, private asset market transactions ultimately are micro level
decisions. The micro level refers to individual assets or deals. At this level, specific transactions are
governed by the “NPV rule” of investment decision-making. This normative principle states that an
investment transaction (whether it is an acquisition or a disposition) should occur only if the transaction
can be made at a net present value (NPV) of at least zero, and this rule of course applies to both parties in
the transaction. For each party, the NPV is the present value of what they are obtaining from the deal,
minus the present value of what they are giving up in the deal. The dollar value of the price at which the
transaction occurs is what the seller obtains, and what the buyer gives up. Label this value Pit for asset i
transacted at time t. The value of what the buyer obtains is his perceived investment value for the asset,
labeled IVbit. The value of what the seller gives up is her perceived investment value for the asset, labeled
IVsit. Thus, for a transaction to make sense:
IVitb − Pit ≥ 0, and
Pit − IVits ≥ 0.
⇔ IVits ≤ Pit ≤ IVitb
In practice, buyers may set their reservation prices below their investment values, if they perceive
the current asset market value as being below the investment value they place on the asset, and they
perceive the current market as being not too difficult (i.e., sufficiently dense, or liquid,--a sufficient
number of sellers of the asset type of interest to the buyer).8 Thus:
RPitb ≤ IVitb
7
For our model to allow for downward-sloping asset demand and upward-sloping asset supply is consistent with
traditional assumptions in much private asset market literature, such as the real estate and housing economics
literature. There is also growing acceptance of such an assumption in the financial economics literature, notably
concerning private equity markets (e.g., see Gompers & Lerner (2000) regarding the venture capital industry), and
even concerning public securities markets. (See, for example, Shleifer (1986).)
8
Why should buyers pay more than they have to, even if the asset would be worth more to them? Buyers wish to
maximize their NPV in the transaction.
9
Similarly, sellers may set their reservation prices above their investment values if they perceive the
current market value as being above the investment value the asset provides to them, and they perceive
the current market as being sufficiently liquid, as indicated by the number of buyers in the market.9 Thus:
RPits ≥ IVits
As reservation prices govern the decision to transact, the micro-level condition determining whether a
transaction will take place for asset i at time t is:
RPitb ≥ Pit , and
Pit ≥ RPits .
(1)
⇔ RP ≤ Pit ≤ RP
s
it
b
it
That is, from the micro-level perspective, a transaction can occur whenever the transaction price Pit lies
above the sellers reservation price RPsit and below the buyers reservation price RPbit. Indeed, according to
our definition of reservation price, a transaction should take place whenever compatible trading partners
find each other. “Compatibility” in this context is defined by condition (1) above. In such conditions, to
fail to transact would be “leaving money on the table”.10
Potential transactions in the asset market during the period of time depicted in Figure 1 are
roughly indicated by the region of overlap between the buyer and seller reservation price distributions.
The number of buyers willing to transact at any price “x” on the horizontal axis is represented by the area
underneath the buyer reservation price frequency distribution to the right of x. The number of sellers
willing to transact at price x is represented by the area underneath the seller reservation price frequency
distribution to the left of x. Thus, the size of the overlap region is a rough indicator of the percentage of
properties that are likely to transact during the period of time represented in the diagram.11 Thus, for a
9
Why should owners sell for less than they have to, even if the asset is not worth that much to them? Sellers wish to
maximize their NPV in the transaction.
10
Note in particular that the concept of reservation price can (and, in principle, should) include a consideration of
the value of “waiting to invest” as described by the real options literature. (See, e.g., MacDonald & Seigel (1986).)
11
Not all buyers and sellers represented in the overlap region will necessarily transact within any given period of
time. Rather, all buyers and sellers with reservation prices in this region have a possibility of achieving a match. The
overlap region is not a distribution of the expected transaction prices. In some pairings within the overlap region
these two parties’ reservation prices will be very close and there won’t be much room for negotiation, while in other
pairings the two reservation prices could be quite far apart (i.e., a buyer from far up to the right end of the overlap
region deals with a seller from far down to the left end of the overlap region).
10
given population of assets, the size of this region represents the degree of liquidity in the asset market.
What will be the mean of the transaction price distribution for the type of asset depicted in Figure
1, during the time period represented in the diagram? Based on condition (1) above, the probability that
asset i sells at price x during time period t is given by the probability of finding parties from the buyer and
seller distributions respectively, such that:
RPitb ≥ x
AND
RPits ≤ x
This probability is equal to:
(
)(
Pr( Pit = x ) = 1 − Fitb ( x) Fits ( x)
)
(2)
where Fbit(x) and Fsit(x) are the cumulative probability distributions (CDF) of the buyer and seller (owner)
populations respectively, evaluated at the price x.12 The mean of this theoretical transaction probability
distribution will be located on the horizontal axis at least roughly near the middle of the overlap region ,
at the value indicated by the point P in Figure 1. This is the value that an empirical transaction pricebased index of the asset market value will tend to estimate for the population of assets depicted in Figure
1 for the time period represented in the figure. With symmetric tails in the reservation price distributions
(as depicted in Figure 1), observed transaction prices will be dispersed around P.
Next, consider what happens to this observed transaction sample over time under the variable
liquidity conditions described at the outset of this section, in which liquidity varies pro-cyclically with the
market cycle over time. This situation is depicted in Figure 2. The top panel shows a base period (time
“t”) when the asset market is normal, characterized by average liquidity. The middle panel depicts a
subsequent period of time (t+1) when the market is up, characterized by above-average liquidity. The
bottom panel depicts a third period of time (t+2) when the market is down, characterized by below
average liquidity. The level of the market prices is indicated by the position of the overlap region along
the horizontal axis. The degree of liquidity is indicated by the size of the overlap region, the larger region
corresponding to a greater number of compatible transaction partners, hence a larger percentage of
12
That is, F(x) is the probability that RP
≤
x.
11
consummated sales. Clearly, in order for this market evolution to conform to the stylized empirical fact of
greater liquidity (i.e., greater volume of transactions) during the up-market period and less liquidity
(lower volume of transactions) during the down-market period, the overlap region must increase in t+1
and decrease in t+2 (in both cases in comparison with the base period t). And in order for the overlap
region to evolve in this manner, it is necessary for the buyer reservation price distribution to move with
the liquidity cycle in a more exaggerated manner than the seller reservation price distribution. Although
both distributions may move in the same direction, the buyer distribution moves farther (or moves first).13
----------------------Insert Figure 2
----------------------In contrast to the empirically observable (variable liquidity) situation depicted in Figure 2, a
hypothetical constant liquidity world is depicted in Figure 3. The constant-liquidity prices that would be
observed in the world depicted in Figure 3 reflect the economic opportunity cost concept described
previously, preserving a constant ease of selling across the cycle. Notice by comparing Figure 2 and Figure
3 that in order to preserve constant liquidity the seller reservation price distribution must move not only in
the same direction but equally as far and as fast as the buyer reservation price distribution. Thus, a crucial
point to note is that constant-liquidity value is essentially defined by the potential buyer population-sellers have to move in lock-step with the buyer population in order to preserve constant liquidity.14
13
There are other alternative models to explain pro-cyclical variable liquidity, but they seem less realistic on a priori
theoretical grounds, or else boil down to effectively the same thing as the model depicted in Figure 2. For example,
pro-cyclical variable liquidity could result from the reservation price distributions retaining their mean values but
spreading out to increase liquidity (due to the increased overlap) and shrinking in to decrease liquidity. This would
imply that buyers and/or sellers become less certain about what the market value is during “up” markets, and more
certain during “down” markets, a pattern which does not seem very realistic. In the real world, bad news seems to
engender much more felt uncertainty among market participants than good news.
Another alternative is to have buyer and seller distributions move equally along the horizontal axis in terms
of their mean values, but to have the total number of buyers increase and decrease in a pro-cyclical manner. In
effect, buyers “come out of the woodwork” during the up market, and retreat out of the picture during the down
market. But this model is effectively the same as the one we are depicting in Figure 2 as far as sellers are concerned.
A larger proportion of the seller distribution transacts during the up market, and the sellers most likely to transact are
those on the lower left tail of the seller reservation price distribution. Such a model would therefore have the same
practical implications as the one depicted in Figure 2 (including similar implications for the construction of our
econometric model in the next section).
14
Note that it is the sellers who must move with the buyers to preserve constant liquidity (that is, the buyers are the
“lead partner” in the dance), and not vice versa, because liquidity refers to the ability to sell assets, and it is the
buyers to whom the sellers must sell in order to liquefy their assets. Another way to see this is to suppose the
opposite. Suppose that we preserved constant liquidity by altering the actual buyers’ distribution so as to have the
12
The result is an evolution of the mean asset transaction price in the constant-liquidity world that
is higher than the observed (variable liquidity) average transaction price during up-markets and lower
than the observed average in down-markets. This is represented in Figure 4, which shows the difference
between the constant liquidity (hypothetical) and variable liquidity (empirically observable) transaction
price distributions and mean values in both the up-market (top panel, Figure 4a) and down-market
(bottom panel, Figure 4b). In Figure 4 we have labeled the empirically observable mean price “P”, and
the hypothetical constant-liquidity mean price “V”.15
---------------------------Insert Figures 3 & 4
---------------------------Observed price movements over time reflect both the common movement in both the buyers and
sellers reservation price distributions as well as the relative movement between the two distributions.
Transaction volume, however, varies over time only in response to relative (or differential) movement
between the buyer and seller reservation price distributions (either toward or away from one another).
Figure 5 shows the difference between empirically observed prices and constant-liquidity values
as we have defined them in a world where the market is cyclical and empirical prices reflect pro-cyclical
variable liquidity. There are two alternative possibilities, represented in their pure forms in Figures 5a and
hypothetical buyers (in a constant liquidity world) follow the sellers in lockstep. Then the constant-liquidity price in
the down market (when the market is relatively illiquid) would be higher than the observed empirical price, because
the seller distribution moves less sensitively than the (actual) buyers’ distribution. (The sellers must move less
sensitively than the buyers, or the variation in liquidity will not be pro-cyclical, that is, liquidity would not be higher
in the up market than in the down market, in contrast to the salient characteristic of most private asset markets.) It is
not compatible with the constant ease of selling basis of our constant-liquidity value definition to construct the
model such that sellers could sell more assets (or sell them faster) at higher prices in a down market. While sellers
would obviously like such a world, it is not realistic (sellers cannot force buyers to buy), whereas sellers could
realistically conform their selling behavior to the changes in the buyer reservation prices (if they wanted to, because
sellers conceivably can force themselves to sell, or to refrain from selling). In other words, sellers really do have the
opportunity to sell more assets in the down market at lower prices, whereas they have no realistic opportunity to sell
more assets in the down market at higher prices (unless demand is a positive function of price at such times, contrary
to our assumption of downward-sloping demand).
15
It is of interest conceptually to see how an informationally efficient public exchange market would be represented
in the market model presented here. The very efficient and effective information aggregation and price discovery
processes of such a market (aided by the homogeneity of shares, the density of trading, and the public doubleauction micro-structure of the market) could be represented as causing both the buyers’ and sellers’ reservation price
distributions to rapidly collapse into a distribution with a very low variance around the empirically observable
exchange price “P” in Figure 1. Thus, heterogeneity across agents’ perceptions of market value is greatly reduced,
effectively preserving liquidity (ease of selling) in both up and down markets.
13
5b. Figure 5a depicts the situation in which the liquidity cycle is coincident with the market cycle in
changes (market direction of movement). In this case constant liquidity values will exhibit a temporally
leading phase-shift in the cycle, as compared to the variable liquidity prices, as shown in Figure 5a. In this
situation, buyers move first, and sellers later catch up. This type of behavior can be thought of as follows.
At the beginning of an upswing, good news arrives (underpinning the upswing). The buyer population
reacts quickly to this good news, moving to the right (that is, increasing their reservation prices, as in the
middle panel in Figure 2 corresponding to time t+1). The sellers at first do not respond or respond more
slowly, not increasing their reservation prices as much. So the two distributions overlap more, causing the
increased volume of transactions (larger overlap triangle) as prices move up. Since the constant-liquidity
value is governed by the movements in the buyer pool, the constant liquidity price moves first in the
cycle, before the observed empirical prices. In general, when prices are moving up, the constant-liquidity
values will lie above the empirical prices, as seen by comparing the middle panels in Figures 2 and 3
(corresponding to period t+1). Similarly, when prices are moving down, the constant-liquidity values will
lie below the empirical prices, as seen by comparing the bottom panels in Figures 2 and 3 (corresponding
to period t+2).
Now look at Figure 5b. This depicts the situation in which the liquidity cycle is coincident with
the market cycle in levels (rather than in movement direction). In this case the constant liquidity values
will exhibit magnified amplitude in the cycle, as compared to the variable liquidity empirical prices, as
shown in Figure 5b. In this situation peak liquidity corresponds to the peak of the market cycle in
observed prices and value levels. So in this case the middle panels in Figures 2 & 3 correspond to the
peak in market values rather than to the period of upward-movement in prices. Thus, constant liquidity
values exceed empirically observable prices at the cycle peak, and they are lower than observed values at
the cycle trough (as in the bottom panel in Figures 2 & 3).
14
---------------------------Insert Figure 5
---------------------------The two alternative models of the liquidity cycle depicted in Figures 5a and 5b raise interesting,
and possibly somewhat differing, questions about how the private asset market functions and what type of
behavior governs its market participants. If the liquidity cycle is coincident with the market in levels (as
in Figure 5b), this implies that buyers and sellers move in terms of revising their reservation prices at the
same time and in the same direction, but with buyers tending to move farther than sellers. Such behavior
might be characterized (perhaps a bit simplistically) as “excitable buyers” and/or “conservative owners”.
If the liquidity cycle is coincident with the market in changes (as in Figure 5a), this implies that buyers
move first, and sellers catch up later. Such behavior might be characterized as “quick buyers” and/or
“slow or sticky-price sellers”, suggesting that buyers either obtain better information sooner than
property owners, or are able to act sooner (in the sense of revising their price expectations). These
alternatives may have different implications for such theories as the “noise-trader” model developed in
the financial economics capital markets. Some of the theories of market functioning in the financial
economics literature suggest “irrational” behavior on the part of some market participants, though the
relevance or importance of such behavior is controversial in the literature.16 These models (along with
much of the financial economics micro-structure theory developed over the past two decades) generally
require heterogeneous information endowments among market participants. Such heterogeneity is easily
accommodated in the buyer and seller reservation price distributions of the market model described here.
Which of the two alternatives depicted in Figure 5 corresponds to the way the liquidity cycle
behaves in actual empirical private asset markets? In fact, it is important to note that the two alternatives
depicted in Figure 5 are not mutually exclusive. We distinguish them merely as “pure types”. It is possible
for market behavior to simultaneously exhibit both types of liquidity cycles, at least to some extent. Thus,
16
See, for example, Shleifer & Summers (1990) in the financial economics literature. Some implications of the
noise-trader model and related developments regarding the functioning of the market for REIT shares are explored
in such recent papers as Ling & Ryngaert (1997), and Clayton & McKinnon (2001). A possible rational explanation
for why buyers would reduce reservation prices farther than sellers on the arrival of bad news is suggested by
Childs, Ott & Riddiough (2002b).
15
constant liquidity values may exhibit both a temporal lead and a magnified cycle amplitude (or increased
volatility), compared to transaction prices in the private asset market. Ideally, empirical analysis would
enable the relative extent of these two effects to be sorted out, as well as a more general quantification of
the magnitude of the difference between observed transaction prices versus constant liquidity values that
hold the ease of selling constant. An empirical index quantifying the percentage changes over time in
constant-liquidity asset market values (or “capital returns”, or “appreciation returns” as they are called in
the real estate investment industry) could help to quantify the economic importance of whatever
behavioral phenomena underlie the trading volume variations observed in private asset markets.
An empirical constant liquidity value index would not only allow a more valid comparison of
asset prices over time (hence, construction of a more meaningful capital returns series) within the private
market, but also would allow better comparisons of asset class risk and return behavior between private
asset markets and publicly-traded securities, enabling such comparisons to be made on a more apples-toapples metric.17 With this motivation we turn our attention in the next section to the development of an
econometric model designed to enable such empirical analysis.
III. An Econometric Model of Variable Liquidity Prices Including Correction for Sample Selection
Bias and an Adjustment to Reflect Constant-Liquidity Values
In this section we develop an econometric model based on the model of market functioning
described in the previous section. Our objective is to enable the empirical estimation of an index of
historical market value changes (or returns) that reflects the constant liquidity value construct defined in the
previous section. The model we describe here also provides for the correction of sample selection bias that
may occur in empirical price indices derived from nonrandom samples of assets that transact during each
period of time. The fundamental data requirement for this model is information on both the sold and unsold
assets each period, within the given population of assets that define the private asset market being studied.
17
Such comparisons would still not be completely perfect apples-vs-apples concepts and measures of returns across
the two asset classes, because the liquidity differences across the two asset classes are not just in the temporal
variation of liquidity, but also in what might be called the “average level” of liquidity, that is, the typical length of
time and expense involved in selling investments.
16
We begin with the specification of the buyer and seller (owner) reservation prices , as described in
Section II:
where:
P + βb Z +εb
RP b =∑
αbj X ijt
∑ t
t
it
it
(3)
P + βs Z +εs
RP s =∑
αsj X ijt
∑ t
t
it
it
(4)
RP b
it
= the natural logarithm of a buyer’s reservation price for asset i as of time t , drawn from the
buyers’ distribution,
b
εit
= a normally distributed mean zero random error,
RP s = the natural logarithm of a seller’s reservation price for asset i as of time t , drawn from
it
the sellers’ distribution
s
εit = a normally distributed mean zero random error,
X P = a vector of j asset-specific cross-sectional characteristics relevant to valuation,
ijt
Z = a zero/one time-dummy variable (=1 in year t).
t
In (3) and (4), the
P
αbj X ijt
∑
and
P
αsj X ijt
∑
components reflect systematic asset-specific effects
common to all potential buyers, and all potential sellers (owners), respectively. There is some temporal
variation possible in the
X P
ijt
the t in the subscript. But the
, (e.g., in the case of real estate, property age would be an example), hence
X P
ijt
are all micro-level asset-specific variables, excluding any market-wide
phenomena or effects, and thus are essentially cross-sectional in nature.18
The dispersion within the buyer reservation price distribution is governed by the dispersion in
b
εit
, while the dispersion within the seller distribution is governed by
s
εit
. These error terms are random,
varying across the individual potential buyers and across individual potential sellers, reflecting
unobservable characteristics of the parties.
b
s
In contrast, the βt and βt coefficients represent systematic and common factors across all
b
s
buyers and all owners (respectively), within each period of time. βt and βt are also common across all
18
For example, in real estate, typical asset-specific variables relevant to value include property type, location, size,
and various measures related to the physical quality of the property. In Gompers & Lerner’s (2000) model of venture
capital firm value, asset (firm) specific variables included measures such as the firm industry, location, and “stage”
of the venture process.
17
assets (i) within each period of time, reflecting the market as a whole (for the population of the type of
assets in question) during period t. The combined effect of the differences between the
b
α
j
and
s
α
j
b
s
coefficients and the βt and βt coefficients is therefore what distinguishes the buyer and seller
reservation price distributions systematically from each other, each period. These population-specific
responses govern where the buyer and seller reservation price distributions are centered (e.g., horizontally
in Figure 1), and serve to keep the buyer RP distribution generally to the left of the seller distribution.
Movements in the market over time are reflected in the βt coefficients, both movements that are
common across buyers and sellers, and differential movements between the two sides of the market. The
b
s
differences between the βt and βt coefficients reflect the difference in the responsiveness of buyers and
sellers to the market’s cycle, consistent with the model of variable liquidity presented in the previous
section. For example, if sellers “move” (in the sense of adjusting their reservation prices) more slowly than
buyers (implying a liquidity cycle coincident with market changes, as in Figure 5a), then the changes in the
βts coefficients will tend to lag behind the changes in the βtb coefficients. As noted in the previous
section, it is such cyclical differential movement of the two distributions over time, relatively toward or
b
away from each other, that causes variable liquidity in the private asset market. The interaction of βt
s
and βt together over time will produce the empirically observed market-wide price movements, derived
from the overlap regions described in Figure 2 in the previous section. As noted there, movements in
constant-liquidity market values are governed by movements in the buyers’ reservation price distribution
b
s
alone, and thus reflect βt , not βt .
Transaction decisions and the resulting observable transaction prices are governed by macro and
micro level considerations as described in the previous section. Assume that a potential seller receives
offers from potential buyers at a rate of one per period. (Units of time can be made arbitrarily small, and we
18
could equivalently assume that a potential buyer finds assets on which to make an offer at a rate of one per
period.) A transaction is consummated if and only if the buyer’s reservation price exceeds the sellers: RPbit
≥ RPsit. Only under this condition do we observe a transaction price, Pit. In other words, consistent with the
NPV decision rule described in Section II:
 observed , if RP b − RP s ≥ 0

it
it
P =
it
b − RP s < 0 .
unobserved
,
if
RP

it
it

(5)
The observed transaction price must lie in the range between the buyer’s and seller’s reservation
prices, both of which are unobserved. The exact price depends on the outcome of a negotiation, and depends
on the strategies and bargaining power of the two parties, a topic beyond the scope of this paper. We assume
that the transaction price will equal the midpoint between the buyer’s and seller’s reservation prices.19
Using (3) through (5) and our midpoint price assumption, we find that among sold assets, the
expected transaction price (for asset i as of time t) is:
[ it ] = 12 ∑ α bj + α sj  X ijtP + 12 ∑  βtb + β ts Z t + 12 E[(ε
EP
j
t
b
it
)
]
+ ε its RPitb ≥ RPits .
(6)
The expected value of the sale price consists of three components: the expected midpoint between the assetspecific buyer and seller perceptions of value, the midpoint between the market-wide buyer and seller
perceptions of value, and the expected value of the random error, which is itself the midpoint between the
buyer’s and seller’s random components among the parties that consummate transactions. This last term is,
in general, nonzero, because of the condition that the buyer’s reservation price must exceed the seller’s
reservation price in any observable consummated transaction.
Taken together, equations (3)-(6) allow a representation of the model of asset value evolution
through time described in section II and summarized graphically there in Figures1 & 2. E[Pit] is the mean of
19
There is no reason to assume that either side of the negotiation will systematically have greater bargaining power
or negotiating ability. Our assumption of trades at the midpoint is more realistic and more general than the
assumption used in many previous studies in the real estate literature that all trades are at the buyer’s offer price, and
the midpoint price assumption is consistent with Wheaton’s (1990) model of the housing market as a double-sided
search market.
19
the transaction price distribution in period t. In theory, if the necessary data are available, then we can
measure E[Pit] by estimating (6) via the following regression:
Pit = ∑ a j X ijtP + ∑ β Z + (ε
t
j
(
t t
)
it
RPitb ≥ RPits )
(
(7)
)
1
1
1
where: a j =  α bj + α sj  , β t = β tb + β ts , and ε it = ε itb + ε its (and recall that Zt is a zero/one time2

2
2
dummy). An estimated hedonic price index could be constructed over time based on such estimation. Note
that the βt coefficients reflect the market movements, the evolution of the observed transaction prices over
time, caused by the interaction between the buyers’ and sellers’ reservation prices. The temporally varying
coefficients βt thus represent the value levels of a log-price index for the market in question, keeping in
mind the observation selection condition represented in (5), that
RP b −RP s ≥0
it
it
.
The stochastic error term in (6) may have a nonzero mean because the observed transaction sample
is not a random sample of the buyer and seller populations. Rather, only selected assets transact, namely,
those for which RPbit
[
]
b
s
b
s
≥ RPsit. If E ( ε it + ε it ) RPit ≥ RPit ≠ 0 , then simple OLS estimation of (7) will
result in biased coefficients.
This sample selection bias problem can be corrected by a procedure developed by Heckman
(1976, 1979) and now widely available in econometric software packages. To be more precise, our model
is a partial observability model of the type referred to as a censored regression model with a stochastic and
unobserved threshold (Maddala, 1985). The data are censored, not truncated, under the assumption that the
characteristics of both sold and unsold assets are observed. The threshold (seller reservation price) is not
observed, and it contains a stochastic term.20
20
This model is frequently applied to labor supply examples where a market wage is observed only if the market
wage offer exceeds a person’s reservation wage. Such a model is very similar to our model (there are buyer and
seller distributions and observability is determined by an equation such as (5)), except we have a different
assumption about the observed transaction price (our midpoint price assumption) and we focus on intertemporal
changes. Nevertheless, the nature of the censoring mechanism is identical. A good discussion of this model, applied
to the labor market example, is presented in section 8.4 of Maddala (1985).
20
To address the sample selection problem, estimation of (7) proceeds in two steps. The first step
estimates a probit model of the decision of whether to sell the asset or not. The latent variable describing the
decision for the i-th asset in period t is
S*
it
:
S * = RP b −RP s
it
it
it
S*
it
is not observable, only the outcome
S
it

 1,
=

0,
S
it
.
(8)
is observed:
if S * ≥ 0
it
if otherwise.
(9)
In other words, a sale occurs if and only if RPbit ≥ RPsit.
Equation (8) defines
S*
it
to equal the difference between the buyer’s and seller’s reservation prices
for the asset. Subtracting (4) from (3) as in (8) yields:
S * =∑
(αb −αs ) X P +∑
( βb −βs ) Z +(εb −εs )
j
j
ijt
t
t
t
it
it
it
.
(10)
b
s
b
s
b
s
We define ω j = α j − α j , γ t = β t − β t , and ηit = ε it − ε it . The Zt variable here is the same as
that in (3), (4), and (7), a zero/one time-dummy variable. Equations (9) and (10) can be estimated as a
probit model: .
∑
Pr[S it =1] =Φ
ω X P +∑
γt Z t 

j ijt



(11)
where Φ[ ] is the cumulative density function (cdf) of the normal probability distribution evaluated at the
P
value inside the brackets, based on X ijt and Z t . The probit model estimates the coefficients and residuals
only up to a scale factor. The estimated coefficient of Zt in (11) is γ t / σ and the estimated error is ηit / σ
2
b
s
, where σ = Var (εit − ε it ) . Label the estimated probit coefficient γˆt , so that:
(
)
γˆt = γ t σˆ = βˆtb − βˆts σˆ .
From the estimation results of the probit, we next create the inverse Mills ratio ( λit ). The inverse
Mills ratio equals the ratio of the pdf to the cdf evaluated at time t for observation i (Maddala, 1985, p. 224).
21
The second step in the Heckman procedure is to estimate an OLS hedonic price equation including
as explanatory variables those listed in equation (7), and λit
.
P
=∑
a X P +∑
βt Z t +σ λ +υ
j
ijt
it
εη it
it
where
σ
εη equals
.
(12)
the covariance of the errors in (7) and (11). As noted by Greene (1991), υit has 0
mean and the above estimation produces consistent estimates of the coefficients, but heteroscedasticity is
present. This can be corrected using weighted least squares as described in Greene (1991).
How can we derive from an empirical (variable liquidity) index such as one based on (12) a
constant-liquidity index that depicts the market value changes across time required to maintain constant
liquidity? To answer this question, we must integrate the variable liquidity model described in Section II
with the econometric model described above. The key to this integration is to recall the point made in the
earlier section that constant liquidity values are governed purely by the buyers’ reservation price
distribution. Thus, changes over time in the mean (or systematic part) of the buyers’ reservation price
distribution equal the changes over time in the constant-liquidity market value that we want to model.
That is:21
Vit − Vit −1 = ∑ α b  X P − X P
j  ijt

+ β tb − β tb−1
ijt − 1 
(13)
The XP part of (13) is only necessary to consider the idiosyncratic effect of time within a particular asset i
that might differ from the general population (i.e., a specific representative asset “i”).22 A market index of
the changes over time in the constant-liquidity market values reflect only the market-wide component of
b
(13). Thus, the βt coefficients trace out the constant-liquidity index over time:
Vt = βtb
21
(14)
Recall that Zt is a zero/one time-dummy variable, so the change in the market value between period t-1 and period
t simply equals the difference between the two time-dummy coefficients.
P
22
For example, in a typical real estate application one of the X ijt variables would typically be property age. To
index the market value change over time of a representative property, the effect of the property’s aging must be
included. On the other hand, an index of the overall property market value changes would not include the age
variable.
22
b
ˆ , and from (6)
An estimate of βt can be derived as follows. First, estimation of (12) yields β
t
we see that:
(
)
βˆ t = (1 2) βˆ tb + βˆ ts
.
⇒ βˆ b = 2 βˆ − βˆ s
t
t
(15)
t
From the probit estimation (11) and its underlying equation (10) we have:
γˆt = ( βˆ tb − βˆts ) σˆ
If we know
σˆ
(16)
we can solve (15) and (16) simultaneously to obtain:
βˆtb = βˆt + 12 σˆγˆt
(17)
Thus, it suffices to add an adjustment term, σˆγˆ / 2 , derived empirically from our probit model
ˆ , derived
of sale probability in equation (11), to the variable-liquidity index log-value level, β
t
empirically from our (selection-corrected) hedonic model of transaction prices. Adding this adjustment
each period converts the variable liquidity index to a constant liquidity index of market values. To find the
value of
σˆ
we must solve for all of the parameters of the model. The solution and conditions for
identification are derived in the appendix.
Consider the intuition behind this liquidity adjustment. The underlying sale explanatory model in
equation (11) is the difference between buyer and seller reservation price as represented by
S*
it
in
b
s
equation (10). Recall that the βt and βt parameters that determine γt in (10) reflect only market-
wide effects on the systematic part of the buyers’ and sellers’ reservation price distributions. (See
equations (3) & (4).) Thus, γt reflects only market-wide effects on the probability of sale. Therefore, the
γt coefficients reflect the market-wide temporal variation in sale probability. In effect, γt can be
(
)
viewed as tracing out an index of market liquidity over time. In (17), the addition of (1 / 2 ) βˆ tb − βˆ ts in
23
γˆ σˆ , to (1 / 2) ( βˆ
the form of 1 t
2
b
t
)
ˆ , adds the missing half of the buyers’ response
+ βˆ ts in the form of β
t
to the market and removes the “unwanted” half of the sellers’ response to the market, to leave us with
only the entire buyers’ response to the market, βˆ tb . It is this buyers’ response that alone governs the
constant liquidity values defined in Section II.
Note that constant-liquidity index values Vt differ from traditional empirical transaction price
index values Pt fundamentally because equation (3) differs from equation (7): buyer reservation prices
differ from empirically observed transaction prices. This is because prices in consummated transactions
reflect the outcome of a negotiation process between the buyer and seller. Thus, empirical prices reflect a
combination of buyer and seller influence. In the previous literature on real estate transaction price-based
indices, models represented by equations (7) or (12) have been estimated with time coefficients of the
ˆ , not adjusted as per (17). Hence, previous studies have been unable to estimate constantform of β
t
liquidity market values as we have defined this concept here. 23
It is also clear from the foregoing analysis that the effect of variable liquidity on empirically
observed prices is a distinct phenomenon from the classical type of sample selection bias addressed in the
Heckman procedure. Merely correcting for selection bias as in (12) still results in a model that reflects
prices defined by equation (7), whereas movements over time in constant liquidity values are governed by
equation (3).
Finally, we relate the empirically-based constant-liquidity value adjustment derived here to the
questions about the functioning of the private asset market that we noted in section II. Liquidity
coincident with market levels, producing constant liquidity values with magnified cycle amplitude
compared to empirical prices, would be evidenced by γˆ t values tending to be greater during market
ˆ are historically high) and less during cycle troughs (when the β
ˆ are low).
cycle peaks (when the β
t
t
23
This point applies both to indices based on the hedonic value model specification and to indices based on the
repeat-sales regression specification.
24
On the other hand, liquidity coincident with market changes, producing constant liquidity values that
ˆ
temporally lead empirical prices, would be evidenced by γˆt values tending to be greater when the β
t
ˆ values are falling ( βˆ − βˆ < 0 ). The
values are rising ( βˆ t − βˆ t −1 > 0 ) and less when the β
t
t
t −1
γˆ σˆ
magnitude of the 1 t
2
adjustment terms in (17) provide a measure of the economic importance of the
variations in liquidity, in terms of the percentage impact such variable liquidity has on market value
changes over time. We argue that such an index would be more appropriate, in some circumstances, for
making comparisons between market value levels across time, and for making comparisons of market
movements or capital returns between private markets characterized by variable liquidity and public
securities markets that are designed to maintain a constant ease of selling.
IV. Empirical Application to NCREIF Commercial Real Estate: Data & Model Specification
The problem of measuring and monitoring changes in investment values has received particular
attention in the private real estate investment industry. In this industry the primary practical solution
developed so far to the problem posed by infrequent trading of unique assets is the development of
appraisal-based indices, most notably, the NCREIF Property Index (NPI). 24 But such indices are
expensive to produce, and have technical shortcomings. In particular, appraisal estimates of value tend to
lag behind market movements and may smooth away some such movements.25
An alternative approach is to use transaction-based indices of commercial property prices,
constructed using statistical procedures based directly and entirely on transaction price data. An appealing
24
The NPI is a quarterly index of U.S. institutionally held commercial investment real estate total returns (broken
out by “income” and “appreciation” components), commencing in 1977, produced by the National Council of Real
Estate Investment Fiduciaries (see www.ncreif.org). The index currently tracks the performance of some 3300
properties, with an aggregate market value in excess of $100 billion, and it is widely used as both an investment
performance benchmark and a general investment research tool for the asset class.
25
Both empirical evidence and optimal appraisal theory support this claim. Regarding appraisal theory, see most
notably: Quan & Quigley (1989, 1991), Geltner (1997), Childs, Ott, & Riddiough (2002a), and Fisher & Ong
(2002). For clinical and empirical evidence of appraisal lag, some recent articles include: Diaz & Wolverton (1998),
Fisher & Geltner (2000), and Clayton, Geltner & Hamilton (2001).
25
feature of transaction-based indices is that they could potentially be based on public and commercially
available data sources, thereby allowing expansion of the population of commercial properties indexed, to
include properties not held by members of NCREIF or other investors willing to incur the expense of
regular, frequent appraisal. Recent articles reporting attempts to develop transaction-based commercial
property indices include Judd & Winkler (1999) and Munneke & Slade (2000, 2001). These studies
focused on the sample selection bias question, and report finding relatively minor bias. However, these
studies were based on specific populations of non-institutional commercial property whose markets may
behave differently than that of the large-scale institutional real estate represented in the NCREIF Index.
None of the transaction-based indices developed previously in either the housing or commercial property
literature have attempted to estimate the price effect of variable liquidity, or to construct a constantliquidity value index.
To demonstrate estimation of the constant liquidity value index described in Section III, we use
data obtained from NCREIF.26 This database includes property-specific information on over 8,500
investment-grade properties that have been held for the tax-exempt members of the NCREIF. These data
have been used to construct the NPI since the fourth quarter of 1977.
The NCREIF portfolio of properties currently (2001:Q4) consists of 3311 properties, with an
aggregate appraised value of just over $100 billion dollars. Properties included in this database are
generally well distributed across the four major regions of the nation. For example, properties located in
the East, Midwest, West, and South represent 22%, 16%, 33%, and 29% of the number of properties in
the database, respectively.27 The current database includes four property types: office (29%), industrial
(29%), apartment (24%), and retail (18%).28
26
The NPI database is proprietary and access limited. Direct access to individual property level data was limited to
only one of the authors of this study, Jeff Fisher, NCREIF Consulting Director of Research & Technology.
27
Properties located in the East and West tend to be of higher values than those located in the South; hence, the
value of the properties located in the East, Midwest, West, and South represent approximately 27, 16, 36, and 21
percent of the aggregate value of the database, respectively
28
Individual office and retail properties are generally higher in value than the industrial and apartment properties.
Office properties represent approximately 42% of the aggregate value of the database, while the industrial, retail,
and apartment property classes represent 18 to 20% each.
26
To develop selection-corrected and constant-liquidity transaction-based indices of the NCREIF
population, data on sold and unsold property must be available. The data in the NCREIF database provide
this type of information, as well as a unique opportunity to compare appraisal-based and transactionbased indices of price movements, including explicit examination of the effect of both sample selection
bias and variable liquidity.
The data set we examine includes all properties in the historical NCREIF database held during
any period between 1982:2 and 2001:4.29 During this period we identify 3,138 properties that sold. In
addition to the transaction observations, the number of unsold properties total 27,254 observations. This
yields a total of 30,392 observations in the data set that we employ.30
The numbers of sold and unsold observations are reported by year in Table 1. As shown, the sales
volume increased from 1983 to 1989 and then declined through 1992. Following 1992, the number of
sales consistently increased again until they peaked in 1997 and then declined though the remainder of the
period studied. Table 1 also indicates that the mean annual price per square foot of the properties that sold
approximately doubled, from $43.83 to $88.57, over the 19-year period (an implied annual rate of
3.77%). Casual observation reveals that the mean size (square footage) of both the sold and unsold
samples increased substantially over the period. Note that the mean size of the sold properties is smaller
than that of the unsold properties in all years except 1988. Finally, Column 8 of Table 1 reports the
number of properties that were acquired by NCREIF members annually. It is especially interesting to note
that the trend in the number of acquisitions is shaped similar to that of the number of sales--increased
acquisitions through 1989, decreases through 1992, followed by increased acquisitions until 1998. This
suggests that acquisitions as well as dispositions reflect the same liquidity cycle.
-------------------------Insert Table 1
29
Individual property characteristics (e.g., square footage) are not available prior to 1982:2; thus, the study period is
restricted to begin in 1983.
30
The number of sold properties is less than the difference between the number of properties that have ever been in
the index and the number currently remaining in the index, because some properties exit the index by other means
than sales (e.g., the NCREIF member owning the property quits NCREIF). The number of observations exceeds the
number of properties in the database because most properties are held more than one year, and we obtain annual
observations of the variable values for each property.
27
-------------------------The major task involved in empirical application of the econometric model described in Section
III is to decide on specifications for equations and (7) and (11), the models of sale price and sale
probability respectively. Our specification of the hedonic value model in equation (7) uses the log of the
price per square foot as the dependent variable in the hedonic value model. The “hedonic” explanatory
variables include six property-type dummy-variables and seven geographical region dummy-variables.31
The most important explanatory variable in our hedonic model is the log of the property purchase price
per square foot. This acts as a “catch-all” or composite hedonic variable, capturing many latent or
unobservable hedonic characteristics, similar to the assessed-value specification proposed by Clapp &
Giacotto (1992).32 Finally, we include a dummy-variable indicating whether the property was held by the
NCREIF member in a joint venture. Joint-venture properties may tend to differ systematically from other
NCREIF properties (they are often acquired in the development phase), and the sale of a joint-venture
property would require approval of all partners in the venture, including some who may be taxable
entities or who would otherwise have different perceptions of investment value than the NCREIF
member. The results of a simple OLS estimation of this hedonic value model are presented in Table 2.
Time is represented by zero/one time dummy-variables corresponding to the calendar years 1984-2001
(1983 is the base year). The resulting transaction price index is thus defined by the estimated coefficients
ˆ . However, this index is not corrected for sample selection bias.
on the time-dummy variables, the β
t
-------------------------Insert Table 2
--------------------------
31
The property-type dummies include: CBD office, Suburban office, regional shopping mall, warehouse, industrial
research & development facility, and industrial flex space facility. The geographical location dummy-variables
include all but one of the eight NCREIF multi-state regional divisions of the U.S.: Northeast, Mideast (similar to the
census Middle Atlantic region), Southeast, Southwest, East North Central, West North Central, Mountain, and
Pacific. (Mountain was the omitted region in the specification, so the regional coefficients represent incremental
differences relative to that region.)
32
For example, the property purchase price will tend to reflect the value effect of such property characteristics as
size, age, physical and location quality, income earning potential, risk, and so forth.
28
For purposes of correcting the preceding index for sample selection bias, and also to estimate the
liquidity adjustments per equation (17), we next specify and estimate a probit model of property sale
probability. The specification of this sample selection model is indicated in general form by equation (11).
The probit model must include the same time-dummy variables used in the hedonic value model. In
addition, the probit model may include cross-sectional variables representing asset-specific characteristics
that are helpful in predicting individual property sale probability.
The specification of this probit model for the NCREIF property population includes a constant,
the annual time dummies, and three cross-sectional variables reflecting asset-specific characteristics,
These three variables include:
•
•
•
Jointven, the previously-described dummy-variable indicating whether the property is held in a
joint venture;
Sqft, the physical size of the property in rentable square feet;
Unleveraged, a dummy-variable indicating that the property has no debt on it (Unleveraged=1
implies an unleveraged investment, no debt encumbrances).
The results of the probit model are presented in Table 3. Although the joint venture variable is
only barely significant, it is included because of it’s a priori theoretical importance for determining sale
probability. Note that the time-dummy coefficients in the probit model (the γˆt ) are almost all
statistically significant, indicating that the liquidity adjustments specified in equation (17) are significant.
-------------------------Insert Table 3
-------------------------The results of the Heckman 2nd-stage OLS hedonic value model, corrected for sample selection
bias by the inclusion of the inverse-Mills ratio (“lambda”) term, are presented in Table 4. Note that the
lambda coefficient is statistically significant, indicating the presence of selection bias in the simple OLS
index reported in Table 2. The time-dummy coefficients in Table 4 represent the selection corrected,
variable liquidity hedonic price index, corresponding to equation (12).
-------------------------Insert Table 4
--------------------------
29
V. Results of the NCREIF Application
The estimated capital returns implied by the uncorrected and selection-corrected variableliquidity transaction price-based indices of NCREIF commercial properties are presented in Table 5,
along with the corresponding returns for the appraisal-based NCREIF Index (NPI). 33 The returns to the
constant liquidity value index constructed by adding the probit-based adjustment terms specified in
equation (17) are also presented in Table 5, along with the capital returns to the NAREIT price index of
publicly-traded real estate investment trusts.34
Table 6 presents a statistical summary comparing the five capital return indices presented in Table
5, and Figure 6 depicts the cumulative log value levels of all five indices. Figures 7-10 present binary
comparisons of the indices starting from the appraisal-based NPI, first comparing with the simple
uncorrected transaction price-based hedonic value index (Figure 7), then comparing that index with the
Heckman index correcting for sample selection bias (Figure 8), next comparing the corrected variableliquidity index with the constant liquidity value index (Figure 9), and finally comparing this index with
the public market-based NAREIT Index (Figure 10).
---------------------------------------Insert Figures 6-10 & Tables 5 & 6
---------------------------------------All five commercial real estate value indices reviewed here present a similar history at the broadbrush level, a history characterized by a very notable cycle, peaking in the mid-to-late 1980s and again in
33
The official NCREIF Index reports quarterly appreciation returns from which a cumulative value level index can
be developed. However, we have modified the official NCREIF Index in two respects to make it more comparable to
the transaction indices we have developed. First, we are using an equal-weighted version of the NCREIF Index
rather than the value-weighting in the official index. Second, we have added back in the capital improvement
expenditures that the official NPI subtracts from the end-of-period appraised value to compute the appreciation
return. We want our version of the NCREIF appreciation index to incorporate the value-enhancing effects of capital
improvement expenditures, as reflected in the actual appraisals of the properties, because the prices on which our
transaction-based indices are based certainly reflect the (market) value of the capital improvements (as perceived by
the buyers and sellers). The result of this second change is that the NCREIF Index depicted in Figure 6 and Table 6
rises a little faster and farther over time than the official NCREIF appreciation index. In addition, we are using
NCREIF appreciation index value levels as of the 3rd quarter each year, for greater comparability with the
transaction-based indices which represent annual average value levels, aggregated across the entire calendar year.
34
This is the All REIT share price index produced by the National Association of Real Estate Investment Trusts
(www.NAREIT.org). We are using the NAREIT Index level as of July 1 each year, to make it more compatible with
the transaction-based indices, for the reason noted previously.
30
the late 1990s (or possibly 2001). All five indices present a very similar long-run trend or average growth
rate over the entire cycle. At a more detailed level, the five indices display interesting differences.
The appraisal-based NCREIF Index presents a clearly smoothed and lagged appearance compared
to the other indices. This is not surprising, given the nature of the appraisal process, and the way the
NCREIF Index is constructed (including some “stale appraisals” each quarter).35
The stock exchange-based NAREIT Index presents a bit of an “odd man out” appearance, with
some movements that are not echoed in any of the other indices. In part, this may reflect fundamental
differences between REITs and direct property investments.36 It may also reflect the effect of the different
type of asset market in which REIT shares are traded. Obviously, the market micro-structure and
functioning of the public stock exchange is very different from that of the private real estate market in
which whole properties are traded. In addition, the investor clienteles are different between these two
types of asset markets. There is some evidence of lack of complete integration between the stock market
and the private real estate market.37 It is interesting to note that in Figure 6 and Table 6 the NAREIT Index
shows some evidence of leading the private market indices in time, particularly in its turning points at the
bottom of the cycle in 1990 and subsequent peak in 1997. This may reflect the greater informational
efficiency of the public stock exchange mechanism, compared to private whole asset markets.
The three transaction-based private market indices behave similarly to each other, tracing out a
pattern roughly in between those of the REIT-based and appraisal-based indices. The transaction-based
indices all display greater volatility and greater cycle amplitude than the appraisal-based index, and they
appear to lead the NPI in time, based on the earlier cycle peak in 1985 (same as the NAREIT 1980s peak)
and the steeper rise out of the early 1990s trough. Unlike the appraisal-based NCREIF Index, but like the
NAREIT Index, the transaction indices all depict a down market during 1999, a period when commercial
35
All properties in the NCREIF Index are supposed to be reappraised at least once per year, and many are
reappraised more often than that. Nevertheless, as not all properties are reappraised every quarter, the NCREIF
Index appreciation level includes the effect of some non-current appraisals each quarter.
36
The types of properties held by REITs are not exactly identical to the types of properties represented in the
NCREIF database. In addition, REIT management policies and considerations (including property trading,
development projects, and financial strategy) add a layer of investment performance results on top of that of the
underlying “bricks & mortar” represented by operating property assets in place.
37
See Ling & Ryngaert (1997), and Ling & Naranjo (1999)
31
real estate securities suffered setbacks due to the 1998 financial crisis and recession-scare, choking off a
major source of capital flow into commercial real estate markets.38 The selection-corrected Heckman
index lags behind the uncorrected transaction-based hedonic index, indicating that NCREIF members
tended to sell their “losers” during the downturn of the early 1990s and to sell their “winners” during the
upswing of the late 1990s.39
Finally, the constant liquidity value index displays greater cycle amplitude and greater volatility
compared to the variable-liquidity transaction price indices. Indeed the constant liquidity value index has
annual volatility almost equal to that of the NAREIT Index (12% for the constant liquidity index versus
13% for NAREIT, compared to less than 10% for the variable-liquidity price indices), and it has a cycle
amplitude even greater than NAREIT in the 1990s upswing. There is also evidence that the constant
liquidity value index leads the variable-liquidity transaction price indices in time, for example in the
earlier peak in 1998 and the slightly faster fall in the late 1980s. It is interesting to relate these
characteristics of the relation between the constant liquidity and variable liquidity indices to the market
functioning behavioral traits described at the end of Section II. The increased amplitude and volatility in
the constant liquidity index is consistent with the “excitable buyers” or “conservative owners” type of
behavior noted in Section II, in which buyers move their reservation prices farther than sellers in response
to news. However, the temporal lead in the constant liquidity index is consistent with “quick buyers”
and/or “slow sellers” (or “sticky prices” among sellers’ reservation prices) type of behavior among private
market participants. In comparing the constant liquidity value index with the selection-corrected variable-
38
Both REIT equity and CMBS debt markets retrenched particularly in the latter half of 1998 and early 1999. Recall
that our transaction-based indices reflect average asset prices aggregated across the calendar years. Thus, the annual
return indicated for 1999 more closely reflects differences between mid-1999 and mid-1998 (rather than end-of-year
based returns).
39
Lower quality properties would tend to suffer the worst performance hit during a severe real estate slump.
Conservative institutional investors such as the pension funds whose capital is managed by NCREIF members may
prefer to unload under-performing real estate during such a period, even though such a disposition policy makes
their investment performance look worse during the down market. They may then try to recoup the performance hit
by selling star properties in the upswing. The overall average growth in the selection-corrected index across the
entire cycle is very similar to the uncorrected hedonic index that directly reflects observed sales, a result consistent
with such behavior.
32
liquidity price index in Figure 10, it seems that both of these types of behaviors are present to some
degree in the institutional commercial real estate market.
VI. Summary
This paper has defined and developed a concept of “constant liquidity value” in the context of a
model of a private asset market that is characterized by pro-cyclical variable volume of trading. We have
characterized the general qualitative implications of this model at the theoretical level. We have
developed an econometric model that enables estimation of empirically-based constant liquidity value
indices of market capital returns or value changes over time, provided data is available on both sold and
unsold assets in the indexed asset population. We have shown how sample selection bias can be
represented and corrected in such a model, a by-product of which is to demonstrate conclusively that
sample selection bias and variable-liquidity price effects are not the same phenomenon, though they are
related, and can be jointly corrected in empirical estimation. The concept, model, and procedure
developed in this paper should be applicable to a range of private asset markets and investment vehicles,
including both commercial and residential real estate, collectibles, and private equity asset classes such as
venture capital.
We have applied this model to the institutional commercial real estate market as represented by
the NCREIF Index. We developed transaction-based indices of the NCREIF property population market
value, including variable-liquidity price indices both without and with correction for sample selection
bias, as well as a constant liquidity value index (that is also corrected for selection bias). We have
compared these transaction-based indices both among each other, and with the appraisal-based NCREIF
Index and the stock market-based NAREIT Index. While all these indices show broad similarities,
significant and interesting differences are apparent. In general, the transaction-based indices show greater
volatility and cycle amplitude, and a temporal lead, compared to the appraisal-based NCREIF Index,
while the NAREIT Index has greater volatility and temporally leads even the constant liquidity value
33
index of the private market. The general pattern of price discovery seems to involve the NAREIT Index
typically moving first, followed by the constant liquidity value index, followed by the variable-liquidity
transaction-based indices, followed last by the appraisal-based NCREIF Index. The total time lag between
NAREIT and NCREIF can be several years, as measured by the timing of the major cycle turning points.
34
Appendix:
Identification of Underlying Market Parameters
In the Censored Regression Model with Stochastic Thresholds
Applied to the Double-sided Search Model of Market Equilibrium
This appendix addresses how the parameters of our double-sided search market model can be
identified. It relies on Maddala (1985, section 8.3 and 8.4) who presents the method of identification for
the standard censored regression model with stochastic thresholds.
2
s
2
b
s
b
First, define: σ s = Var (ε it ) , σ b = Var (ε it ) , and σ sb = Cov(ε it , ε it ) . With this notation, the
2
2
2
value of the scaling parameter in the probit equation is σ = σ b + σ s − 2σ sb , based on (10). The goal is
to solve for σ 2 and use its value in (17) to solve for the constant liquidity price index.
Identification in this model requires one of two possible conditions: either σ sb = 0 or at least
one variable is included in the buyer’s reservation price that is not included in the seller’s reservation
price (or vice versa).40 We assume that there is random matching of buyers and sellers in our model, thus
their pricing errors are uncorrelated in the original uncensored reservation price distributions, hence
σ sb = 0 . This implies σ 2 = σ b2 + σ s2 .
Johnson and Kotz (1972, pp. 112-113) show that the expected value of the variance of the pricing
errors in the set of transactions is:
2
E (ε it2 | S = 1) = σ ε2 − σ εη
(Σγ t Z t )λit
(A-1)
2
b
s
2
2
where σ ε = Var ((ε it + ε it ) / 2) = (σ b + σ s ) / 4 because σ sb = 0 .
∧2
Define E (ε 2 | S = 1) = ε it . Thus,
it
2
∧
ε it is the expected value of the square of the residuals in the
2
selection bias corrected hedonic price equation (12). Solving (A-1) for σε yields:
2
∧
∧ 2
∧
(A-2)
σ ε = (1 / N )[ε it2 + σ εη (Σ γ t Z t ) λ it ]
40
b
This latter condition would be met, for example, if, in equations (3)&(4), for some variable j, α j = 0 and
α sj ≠ 0 , or vice versa.
35
where N is the number of observations used to estimate the hedonic price model.
∧
Previously we reported how λit is calculated and we identified σ εη as the estimated coefficient
of λit (Maddala, p.224, eqn. (8-9)). Thus, all of the right hand side variables and parameters in (A-2) are
2
known once the selection model is estimated. Thus we can derive the value of σε . This value is
routinely calculated in selection correction packages and its square root, the standard error of the estimate
2
2
corrected for selection bias, is reported. Combining the two expressions for σ b + σ s , we find that
σ 2 = 4σ ε2 , or
∧
σ = 2σ ε .
(A-3)
This value can then be used in (17) to adjust the variable liquidity price index to reflect constant liquidity
values.
∧
Other parameters in the model are also of interest. The coefficient of lambda, σ εη , can be
∧
expressed as: Cov[( ε itb + ε its ) / 2, (ε itb − ε its ) / σ ] . This expression simplifies when σ sb = 0 to:
∧
∧
σ εη = (σ b2 − σ s2 ) / 2 σ .
(A-4)
Thus, the coefficient of the inverse Mills ratio ( λit ) informs us about the relative sizes of the variances
of the distributions of the sellers’ and buyers’ reservation price dispersions. If the buyers have a greater
variance, then we expect the coefficient of the selection correction variable to be positive, and vice versa.
From (A-4) we obtain an expression for the difference in variances between buyers and sellers
∧ 2
∧ ∧
price distributions: σ 2 = 2 σ σ εη + σ 2 . Previously, we found that σ 2 = σ − σ 2 . Solving these two
b
s
b
s
2
2
equations for σb and σs we find:
36
∧ ∧
(A-5)
σ b2 = σ σ εη + σ 2 / 2
∧ ∧
(A-6)
σ s2 = −σ σ εη + σ 2 / 2
37
References
Bailey, M, R. Muth & H. Nourse, “A Regression Method for Real Estate Price Index Construction”
Journal of the American Statistical Association 58: 933-942, 1963.
Bryan, T. & P. Colwell, “Housing Price Indices”, in C.F. Sirmans, ed., Research in Real Estate, Volume 2,
JAI Press, Greenwich, CT, 1982.
Case, K. & R. Shiller: "Prices of Single Family Homes Since 1970: New Indexes for Four Cities", in the
New England Economic Review pp.45-56, Sept/Oct 1987.
Childs,P., S.Ott, & T.Riddiough, “Optimal Valuation of Noisy Real Assets”, Real Estate Economics
forthcoming, 2002a.
Childs,P., S.Ott, & T.Riddiough, “Optimal Valuation of Claims on Noisy Real Assets: Theory & an
Application”, Real Estate Economics forthcoming, 2002b.
Clapp, J. & Giacotto, “Estimating Price Indices for Residential Property: A Comparison of ‘Repeat-Sales
and Assessed Value Methods”, Journal of the American Statistical Association 87:300-306, June 1992.
Clayton,J., D.Geltner & S.Hamilton, “Smoothing in Commercial Proeprty Valuations: Evidence from
Individual Appraisals” Real Estate Economics 29(3):337-360, Fall 2001.
Clayton, J. & G. McKinnon, “Explaining the Discount to Net Asset Value in REIT Pricing: Noise or
Information?” RERI Working Paper, 2001.
Court, A. 1939. “Hedonic Price Indexes with Automotive Examples.” in The Dynamics of Automotive
Demand, General Motors Corporation, New York.
Diaz, J. & M.Wolverton, “A Longitudinal Examination of the Appraisal Smoothing Hypothesis” Real
Estate Economics 26(2):349-358, 1998.
Fisher, J., D. Geltner, and B. Webb. “Value Indices of Commercial Real Estate: A Comparison of Index
Construction Methods,” Journal of Real Estate Finance and Economics, 9: 137-164, 1994.
Fisher, J. and D. Geltner, “De-Lagging the NCREIF Index: Transaction Prices and Reverse-Engineering”,
Real Estate Finance 17(1):7-22, Spring 2000.
Fisher,J. & S.Ong, “Optimal Trade-off Between Random Error and Temporal Bias in Selection of
Appraisal Comps”, working paper presented at the AREUEA Annual Meeting, Atlanta, January 2002.
Gatzlaff, D., and D. Geltner. “A Transaction-Based Index of Commercial Property and its Comparison to
the NCREIF Index,” Real Estate Finance, 15: 7-22, 1998.
Gatzlaff, D., and D. Haurin. “Sample Selection Bias and Repeat Sale Index Estimates,” Journal of Real
Estate Finance and Economics, 14: 33-50, 1997.
Gatzlaff, D., and D. Haurin. “Sample Selection and Biases in Local House Value Indices,” Journal of
Urban Economics, 43: 199-222, 1998.
38
Geltner,D. “The Use of Appraisals in Portfolio Valuation and Index Construction”, Journal of Property
Valuation & Investment 15(5):423-447 (www.mcb.co.uk/jpvi.htm), 1997.
Goetzmann, W. “The Accuracy of Real Estate Indices: Repeat-Sale Estimators” Journal of Real Estate
Finance & Economics 5(1):5-54, March 1992.
Gompers, P. & J. Lerner “Money Chasing Deals? The Impact of Fund Inflows on Private Equity
Valuations”, Journal of Financial Economics 55:281-325, 2000.
Greene, W., Economic Analysis, 4th Ed. Prentice Hall, Upper Saddle River, NJ, 1999.
Griliches, Z., and I. Adelman. 1961. “On an Index of Quality Change.” Journal of the American
Statistical Association, 56: 535-548.
Heckman, J. “The Common Structure of Statistical Models of Truncation, Sample Selection and Limited
Dependent Variables and a Simple Estimator for such Models,” Annals of Economic and Social
Measurement, 5: 475-492.
Heckman, J. “Sample Selection Bias as a Specification Error,” Econometrica, 47: 153-161, 1979.
Johnson, N. and S. Kotz. Distributions in Statistics: Continuous Multivariate Distributions, New York,
Wiley, 1972.
Judd, G. D., & D. Winkler, “Price Indexes for Commercial and Office Properties: An Application of the
Assessed Value Method” Journal of Real Estate Portfolio Management 5(1), 1999.
Ling, D. & M. Ryngaert, “Valuation Uncertainty, Institutional Involvement, and the Underpricing of
IPOs: The Case of REITs”, Journal of Financial Economics 43(3):433-456 March 1997.
Ling, D. & A. Naranjo, “The Integration of Commercial Real Estate Markets and the Stock Market” Real
Estate Economics 27(3): 483-516, Fall 1999.
McDonald, R. and D. Siegel "The Value of Waiting to Invest" Quarterly Journal of Economics 101: 707728, November 1986.
Maddala, G. S., "Limited-Dependent and Qualitative Variables in Econometrics," Econometric Society
Monographs, Cambridge University Press, New York, NY. 1985.
Munneke, H. & B. Slade, “An Empirical Study of Sample Selection Bias in Indices of Commercial Real
Estate”, Journal of Real Estate Finance & Economics 21(1), 2000.
Munneke, H. & B. Slade, “A Metropolitan Transaction-Based Commerical Price Index: A Time-Varying
Parameter Approach”, Real EstateEconomics 29(1): 55-84, 2001.
Palmquist, R., "Alternative Techniques for Developing Real Estate Price Indexes." Review of Economics
and Statistics. 62: 267-271. 1979.
Quan,D. & J.Quigley, “Inferring and Investment Return Series for Real Estae from Observtions on Sales”
Real Estate Economics 17(2):218-230, Summer 1989.
39
Quan,D. & J.Quigley, “Price Formation & the Appraisal Function in Real Estate Markets” Journal of
Real Estate Finance & Economics 4(2): 127-146, 1991.
Rosen, S. “Hedonic Prices & Implicit Markets” Journal of Political Economy 82:33-55, 1974.
Shiller, R. "Arithmetic Repeat Sales Price Estimators" Journal of Housing Economics 1(1):110-126,
March 1991.
Shleifer, A., “Do demand curves for stocks slope down?” Journal of Finance 41: 579-590, 1986.
Shleifer, A. & L. Summers, “The Noise Trader Approach to Finance”, Journal of Economic Perspectives
4(2):43-48, 1990.
Wheaton, W. “Vacancy, Search, and Prices in a Housing Market Matching Model”, The Journal of
Political Economy 98(6):1270-1292, December 1990.
40