1. No category

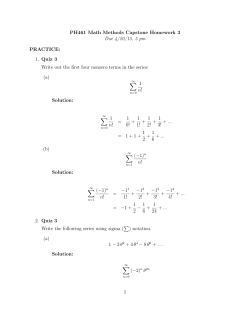
Math 241: Problem of the day
• Midterm 2, October 21. See Exam 2 webpage for info.
• Modified office hours this week and next. See diary.
• Friday: last day to drop the course.
www.math.uiuc.edu/∼clein/classes/2014/fall/241.html
Multiple integrals
Problem: How do we calculate the volume of the solid in R3
above the rectangle
R = [0, 1] × [0, 2] = {(x, y ) | 0 ≤ x ≤ 1 and 0 ≤ y ≤ 2}
in the xy -plane, and below the graph z = x 2 + y 2 + 1?
Solution: Approximate by volumes of boxes and take a limit.
ZZ
f (x, y ) dA =
lim
|∆x|,|∆y |→0
R
www.math.uiuc.edu/∼clein/classes/2014/fall/241.html
X
i,j
f (xi∗ , yj∗ )∆x∆y .
Iterated integrals.
But how do we calculate? Slice, integrate, integrate.
Theorem (Fubini) For R = [a, b] × [c, d] and f : R → R
continuous, we have
ZZ
b
Z
d
Z
f (x, y ) dA =
f (x, y ) dy
a
R
Z
dx
c
d
Z
=
b
f (x, y ) dx dy .
c
www.math.uiuc.edu/∼clein/classes/2014/fall/241.html
a