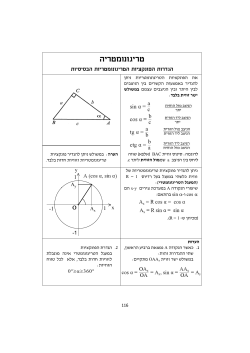
. למכונית שעבר עד למפגש בין מכונית ( שעות (הזמן את
1 בגרות עה מאי 15מועד קיץ א שאלון 35806 א .נסמן ב t -את הזמן )שעות( שעבר עד למפגש בין מכונית Iלמכונית . II נכניס את הנתונים לטבלה מתאימה: מהתחלה עד למפגש בין מכונית IIIלמכונית II זמן t - שעות מהירות v - קמ"ש דרך -מרחק s - ק"מ מכונית I t 50 50t מכונית II t 40 40t המשוואה הראשונה נבנית על פי המרחק בין מכונית Iלמכונית , IIשהוא 15ק"מ. 40t 15 50t 15 10t t 1.5 שתי המכוניות נפגשו לאחר שעה וחצי. ניתן היה גם לומר ,שכיוון שהפרש המהירויות הוא 10קמ"ש, אז 1.5שעות 15 :10 הוא הזמן הנדרש ליצירת הפרש המרחקים. מכונית IIעברה עד למפגש עם מכונית 60 IIIק"מ , 40 1.5 שזה גם המרחק שעברה מכונית IIIבשעה אחת )כי יצאה חצי שעה לאחריה(, ומכאן שמהירותה של מכונית IIIהיא 60קמ"ש. תשובה :מהירותה של מכונית IIIהיא 60קמ"ש. ב .נבדוק האם ייתכן שהמרחק בין מכוניות IIIו I -שווה למרחק שבין מכוניות IIו. I - נסמן ב s -את הזמן שעבר מיציאת שתי המכוניות הראשונות ועד לזמן בו המרחקים שווים. ) (1לפני הפגישה בין מכונית IIIלמכונית : I המשוואה המתאימה. 50 s 60( s 0.5) 50 s 40 s : ונקבל : 10 s 30 10 s s 1.5 אולם זה הזמן שבו מכונית Iומכונית IIנפגשו ,כלומר לפני שמכונית IIIנפגשה עם מכונית , II ולכן לא מתאים לנדרש. ) (2אחרי הפגישה בין מכונית IIIלמכונית : I המשוואה המתאימה. 60( s 0.5) 50 s 50 s 40 s : ונקבל 10 s 30 10 s :ואין פתרון. תשובה :לא ייתכן. נכתב ע"י עפר ילין 2 בגרות עה מאי 15מועד קיץ א שאלון 35806 א .נתונה סדרה הנדסית אין -סופית יורדת , a1 , a2 , a3 , ...שכל איבריה חיוביים ולכן . 0 q 1, an 0 2 כל איבר בסדרה זו )חוץ מהראשון( הוא 5 מסכום שני האיברים הסמוכים לו, לכן an 0.4(an 1 an 1 ) :עבור . n 1 נמצא את מנת הסדרה. ) an 0.4(an 1 an 1 an an q ) / : an 0 q (an 0.4 1 ) 1 0.4( q q 0.4q 2 q 0.4 0 0 q 1 q2 q 0.5 תשובה :מנת הסדרה anהיא . 0.5 an 1 ב (1) .נתונה הסדרה (an ) 2 1 2an bn an q (an ) 2 . bn נראה שהסדרה היא סדרה הנדסית. bn 1 bn 1 2an 1 2an 1 bn 2an 1 2an bn 1 b 1 n 1 2 bn 0.5 bn תשובה :הסדרה bnהנדסית ,כי המנה בין כל שני איברים עוקבים קבועה ) .( qb 2 ) (2נתון כי S10 20, 460בסדרה . bn 20, 460 1023b1 )b1 (210 1 2 1 20, 460 b1 20 1 על פי הקשר בין anל: an - 40 a1 1 2a1 20 1 1 S 40 נחשב את סכום כל האיברים בסדרה : an 1 0.5 20 1 תשובה :הסכום הוא 20 . נכתב ע"י עפר ילין 3 בגרות עה מאי 15מועד קיץ א שאלון 35806 א .מספר הספרות הזוגיות הוא . 3 נסמן ב x -את מספר הספרות האי -זוגיות ,ולכן מספר הספרות הכולל הוא . x 3 מספר אי -זוגי מתקבל אם הספרה השנייה שיוני בוחר היא אי -זוגית. לכן ,מספר זה יתקבל אם יוני יבחר ספרה זוגית ראשונה ושנייה אי -זוגית או שתי ספרות אי זוגיות. נשים לב שההוצאה היא ללא החזרה ,ולכן לאחריה נשארות x 2ספרות. 4 3 x x x 1 7 x3 x2 x3 x2 )4 3 x x( x 1 )7 ( x 3)( x 2 ))4( x 3)( x 2) 7(3 x x( x 1 ) 4( x 2 5 x 6) 7(2 x x 2 0 3 x 2 6 x 24 x natural x 2 x4 תשובה :מספר הספרות האי -זוגיות בקבוצה הנתונה הוא . 4 ב .נמצא את ההסתברות ששתי הספרות שיוני בחר הן זוגיות ,אם ידוע שהמספר שנוצר הוא זוגי. 3 על פי הנתון בסעיף א :ההסתברות שהמספר שנוצר הוא זוגי היא 7 3 2 1 האפשרות ששתי הספרות הן זוגיות היא : 7 6 7 . . 1 1 לכן ההסתברות המבוקשת היא. 7 : 3 3 7 3 2 ) P(2 even digits even number 1 7 6 p (2 even digits / even number ) ניתן גם ,כמובן , 3 2 4 3 ) P(even number 3 7 6 7 6 1 תשובה :ההסתברות היא 3 . ג .אמילי בוחרת שלוש ספרות ,אולם כיוון שנתון כי הספרה הראשונה )ספרת המאות( היא זוגית, הרי שיש לחשב הסתברות לכך שסכום שתי הספרות הבאות הוא זוגי – ואז סכום שלוש הספרות יהיה גם זוגי. כיוון שאמילי הוציאה ספרה זוגית – נותרו 2ספרות זוגיות ו 4 -ספרות אי -זוגיות. סכום שתי הספרות יהיה זוגי – אם שתיהן תהיינה זוגיות ,או ששתיהן תהיינה אי-זוגיות. 2 1 4 3 7 6 5 6 5 15 p ( sum is even number ) 7 תשובה :ההסתברות היא 15 . נכתב ע"י עפר ילין 4 בגרות עה מאי 15מועד קיץ א שאלון 35806 PA .1משיק למעגל בנקודה PB .2 Aמשיק למעגל בנקודה O .3 Bמרכז המעגל. עבור ב. ACD ACB 90 .4 : צ"ל :א PO AD .ב ADC POB .ג DEC DPB .דAC = 2EC . הסבר נימוק טענה 1 5 PAמשיק למעגל בנקודה A נתון 2 6 PBמשיק למעגל בנקודה B נתון 3 7 Oמרכז המעגל נתון 7 ,6 ,5 8 AOP = BOP = 8 9 AOB = 2 9 ,7 10 ADB = 10 ,8 11 ) ADB = POBז( 11 12 PO AD 4 13 ACD ACB 90 7 ,6 14 PBO 90 14 ,13 15 ) ACD PBOז( 15 ,11 16 ADC POB 3 17 ) EDC PDBז( 17 ,15 18 DEC DPB 16 19 17 20 20 ,7 21 21 22 אם מנקודה יוצאים שני משיקים למעגל ,אז הקטע שמחבר אותה למרכז המעגל חוצה את הזווית המרכזית המתאימה +סימון סכום זוויות זווית היקפית שווה למחצית הזווית המרכזית הנשענת על אותה קשת AB כלל המעבר אם זוויות מתאימות שוות אז הישרים מקבילים מ.ש.ל .א נתון המשיק מאונך לרדיוס בנקודת ההשקה כלל המעבר משפט דמיון זווית זווית מ.ש.ל .ב זווית משותפת משפט דמיון זווית זווית מ.ש.ל .ג AD AC DC PO PB OB DE DC EC DP DB PB DC EC 2OB PB DC 2EC OB PB יחסי צלעות מתאימות במשולשים דומים יחסי צלעות מתאימות במשולשים דומים קוטר המעגל שווה לשני רדיוסים והצבה חישוב 22 ,19 23 AC 2EC PB PB כלל המעבר 23 24 AC 2EC חישוב מ.ש.ל .ד נכתב ע"י עפר ילין 5 בגרות עה מאי 15מועד קיץ א שאלון 35806 א ABCD .טרפז ,שבו . BC AD CE BDולכן המרובע BCEDהוא מקבילית. ) DB 1.8ACנתון( ) AC xסימון( ובהתאם . BD 1.8x ) CE = BDצלעות נגדיות שוות במקבילית( ולכן גם . CE 1.8x ) BDA CEA זוויות מתאימות שוות בין ישרים מקבילים(. . CAD DBC 2 ACEעל פי משפט הסינוסים: AC CE sin sin 2 2sin cos 1.8 x sin x 25.84 0 90 תשובה. 25.84 : ב .נתון 87.873 :סמ"ר . S ACE . ACE 180 3 25.84 102.47 AC CE sinACE 2 x 1.8 x sin102.47 87.873 2 2 100 x S ACE 10ס"מ x נוריד גובה CTשל הטרפז מהקודקוד . C 18ס"מ . CE 10 1.8 CTEישר זווית: CT CE 18sin 25.84 CT sin 25.84 7.845ס"מ CT תשובה :גובה הטרפז הוא 7.845ס"מ. נכתב ע"י עפר ילין 6 בגרות עה מאי 15מועד קיץ א שאלון 35806 sin x 3 f ( x) והתחום א .נתונה הפונקציה: 4 cos 2 x .0 x ) (1נמצא את תחום ההגדרה cos 2 x 0 2x k 2 x k 4 2 3 x , x 4 4 3 בתחום הנתון , x 4 4 3 תשובה, x : 4 4 .x . 0 x 3 ) (2תשובה :האסימפטוטות האנכיות הן הישרים , x 4 4 .x ) (3נמצא תחילה את ערך הפונקציה בנקודת הקצה ,שהיא נקודת מינימום על פי הציור: sin 0 ) 0 (0, 0 cos 2 0 f (0) נמצא את נקודת המקסימום: sin 2 x 2sin x cos x cos x cos 2 x 2sin x sin 2 x (cos 2 x) 2 f '( x) cos x cos 2 x 4sin 2 x cos x (cos 2 x) 2 f '( x) )cos x(cos 2 x 4sin 2 x (cos 2 x) 2 f '( x) cos x 0 sin )2 1 ( , 1 x k f ( ) 2 2 2 ) cos(2 2 הביטוי cos 2 x 4sin 2 xחיובי ,כי . cos 2 x 4sin 2 x 1 2sin 2 x 4sin 2 x 2sin 2 x 1 3 x הוא הפתרון היחידי בתחום , x 4 4 2 .0 x תשובה (0, 0) :מינימום ( , 1) ,מקסימום. 2 נכתב ע"י עפר ילין ב .נצייר את הסקיצה של פונקציית הנגזרת ). f '( x תחומי החיוביות /שליליות שלה תואמים את תחומי העלייה /ירידה של ). f ( x 3 לכן ,היא חיובית עבור 0 x או , x ושלילית עבור x 2 2 4 2 4 )cos 0 (cos(2 0) 4sin 2 0 כמו כן 1 (cos(2 0)) 2 , f '(0) ולכן ) f '( xנוגעת בציר ה y -בנקודה ) , (0,1נקודת הקצה שלה. 3 האסימפטוטות האנכיות הן עדיין , x 4 4 ,x שכן שיפועי ) f ( xשואפים ל -בסביבות הישרים. תשובה :הסקיצה משמאל. ג .נתונה הפונקציה ) g ( xהמקיימת ). g ( x) 2 f ( x) f '( x . g (0) 2 f (0) f '(0) 2 0 1 0 בתחום 6 g ( x) 0 x חיובית כי ) f ( xחיובית ועולה ,על פי הציור הנתון, ולכן השטח המוגבל על ידי גרף הפונקציה , על ידי ציר ה x -והישר 6 x הוא מעל ציר ה. x - נחשב את גודלו על ידי זיהוי הנגזרת הפנימית של ). f ( x 6 0 6 0 S (2 f ( x) f '( x) 0) dx f '( x)) dx S (2 f ( x) 1 6 2 f ( x) 2 0 2 S sin 6 )2 0 1 0 1 ( S f 2 ( ) f 2 (0) 6 cos 3 S 1 תשובה :גודל השטח הוא 1יח"ר. נכתב ע"י עפר ילין . 7 בגרות עה מאי 15מועד קיץ א שאלון 35806 ( x 2)2 א (1) .נתונה הפונקציה ( x 1)3 a 0 , f ( x) המכנה מתאפס עבור x 1ולכן תחום ההגדרה הוא . x 1 תשובה. x 1 : ( x 2)2 x2 1 ) lim 3 lim 0 (2 , limלכן y 0אסימפטוטה אופקית. x ( x 1)3 x x x x ( x 2)2 9 lim x 1 ( x 1)3 0 ( x 2)2 9 , lim לכן x 1אסימפטוטה אנכיות. x 1 ( x 1)3 0 תשובה y 0 :אסימפטוטה אופקית x 1 ,אסימפטוטה אנכית. ) (3נמצא את שיעורי נקודות החיתוך עם ציר ה. x - / ( x 1)3 ( x 2) 2 ( x 1)3 0 0 ( x 2) 2 )x 2 (2, 0 (0 2) 2 4 נקודת חיתוך עם ציר ה 4 (0, 4) : y - 3 1 )(0 1 f (0) תשובה. (2, 0) , (0, 4) : ) (4נמצא את שיעורי נקודות הקיצון ואת סוגן. 2( x 2)( x 1)3 3( x 2) 2 ( x 1) 2 ( x 1)6 f '( x) ))( x 2)( x 1) 2 (2( x 1) 3( x 2 ( x 1)6 f '( x) )( x 2)( x 8 ( x 1) 4 f '( x) )x 2 0 x 2 (2, 0 4 ) 81 x 8 0 x 8 (8, הביטוי האלגברי ) ( x 2)( x 8במונה הוא של פרבולה הפוכה )בעלת מקסימום( 4 הנגזרת עוברת משליליות לחיוביות עבור x 8ו) - 81 (8, נקודת מינימום. הנגזרת עוברת מחיוביות לשליליות עבור x 2ו (2, 0) -נקודות מקסימום. 4 תשובה (2, 0) :נקודת מקסימום) , 81 (8, נקודות מינימום. נכתב ע"י עפר ילין ) (5סרטוט הסקיצה המתאימה ,כולל סימון מיקום משוער של שתי נקודות הפיתול: ב .שתי נקודות הפיתול מסומנות בסקיצה :אחת בתחום 8 x 2והשנייה בתחום . x 8 הראשונה בתחום בו הפונקציה עוברת מקעירות כלפי מעלה לקעירות כלפי מטה ,בין נקודות הקיצון. השנייה בשל המעבר לקעירות כלפי מטה בשאיפה לאסימפטוטה , y 0 תשובה :אחת בתחום 8 x 2והשנייה בתחום . x 8 24 ג .שטח המשולש ABOשווה ל 4 - 2 . כיוון שהפונקציה קעורה כלפי מטה בתחום , 2 x 0 אז הגרף של ) f ( xבתוך המשולש, ולכן השטח המוגבל על ידי ) f ( xוהצירים קטן מ. 4 - תשובה :קטן מ. 4 - נכתב ע"י עפר ילין 8 בגרות עה מאי 15מועד קיץ א שאלון 35806 1 א .נתונה הפונקציה a 0 ) f ( x) x 3 a 2 x a 2הוא פרמטר(. 3 נראה כי ערך הפונקציה בנקודת המקסימום שלה הוא חיובי. f '( x) x 2 a 2 0 x2 a2 1 2 2 )x a y a 3 a 2 a a 2 a 3 a 2 a 2 ( a 1 3 3 3 1 2 2 )x a y ( a )3 a 2 ( a ) a 2 a 3 a 2 a 2 ( a 1 3 3 3 גרף הנגזרת הוא של פרבולה בעלת מינימום )"צוחקת"(, לכן הנגזרת עוברת מחיוביות לשליליות עבור , x aוזה שיעור ה x -של נקודת המקסימום. 2 שיעור ה y -הוא ) , a 2 ( a 1וכיוון ש a 0 -נקבל ש. y 0 - 3 תשובה :הוּכַח. ב .הנגזרת עוברת משליליות לחיוביות עבור , x aוזה שיעור ה x -של נקודת המינימום. 2 2 שיעור ה y -הוא ) , a 2 ( a 1וסימן ערכו נקבע על ידי הביטוי , a 1 3 3 המיוצג על ידי קו ישר יורד ,ומתאפס עבור . a 1.5 ) (1נקודת המינימום על ציר ה x -עבור . a 1.5 ) (2נקודת המינימום מעל ציר ה x -עבור ) 0 a 1.5נתון כי .( a 0 ) (3נקודת המינימום מתחת לציר ה x -עבור . a 1.5 ג .הגרפים המתאימים: עבור a 1.5 עבור 0 a 1.5 1 3 ד .נשים לב כי המשוואה x x 1 0 3 מתאימה ל f ( x) 0 -עבור . a 1 על פי הגרף המתאים )האמצעי ,עבור ( 0 a 1.5יש רק פתרון אחד. תשובה :פתרון אחד. נכתב ע"י עפר ילין עבור a 1.5
© Copyright 2025